Dạng 3. Tổng hợp có đáp án
-
615 lượt thi
-
4 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC điểm D thuộc cạnh BC. Từ D kẻ đường thẳng song song với cạnh AB, cắt cạnh AC tại E và đường thẳng qua D song song với AC cắt AB tai F. Chứng minh hai điểm E và F đối xứng với nhau qua trung điểm I của đoạn thẳng AD.
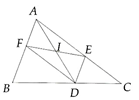
Ta chứng minh được AEDF là hình bình hành => AD EF = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I.
Câu 2:
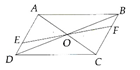
Do E,O, F thẳng hàng mà B, O,D cũng thẳng hàng nên (2 góc đổi đỉnh)
=> DOE = BOF (g-c-g)
=> OE = OF.
Vậy E đối xứng với F qua O.
Câu 3:
Cho góc xOy. Điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy. Tính số đo góc xOy để B đối xứng với C qua O.
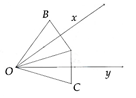
Câu 4:
Cho tam giác ABC. Vẽ điểm D đối xứng với B qua A, vẽ điểm E đối xứng với C qua A. Gọi M là điểm nằm giữa B và C. Tia MA cắt DE tại N. Chứng minh MC = NE.
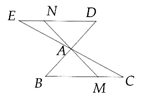
Chú ý: BEDC là hình bình hành
Ta có: EAN = CAM (g - c - g) => NE = MC
