Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 3)
-
2148 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
a) 4x(5x – 2);
b) 7x(3x2– 6x + 2);
c) (x – 5)(x – 7) – x2.
Hướng dẫn giải
a) 4x(5x – 2) = 20x2– 8x
b) 7x(3x2– 6x + 2) = 21x3– 42x2+ 14x
c) (x – 5)(x – 7) – x2
= x2– 7x – 5x + 35 – x2
= – 12x + 35
Câu 2:
a) 6x + 18;
b) 8x2y – 12xy2;
c) x2– 18x + 81;
d) x4y2+x4– 5y2– 5.
Hướng dẫn giải
a) 6x + 18 = 6(x + 3)
b) 8x2y – 12xy2= 4xy(2x – 3y)
c) x2– 18x + 81 = (x – 9)2
d) x4y2+x4– 5y2– 5
= x4(y2+ 1) – 5(y2+ 1)
= (y2+ 1)(x4– 5)
Câu 3:
a) x(x – 6) – x2= 18;
b) 25x2– 64 = 0.
Hướng dẫn giải
a) x(x – 6) – x2= 18
⇔ x2– 6x – x2= 18
⇔ – 6x = 18
⇔ x = – 3
Vậy x = –3.
b) 25x2– 64 = 0
⇔ 25x2– 82= 0
⇔ (5x – 8)(5x + 8) = 0
\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}5x - 8 = 0\\5x + 8 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \frac{8}{5}\\x = - \frac{8}{5}\end{array} \right.\end{array}\)
Vậy \(x = \pm \frac{8}{5}\).
Câu 4:
Cho ∆DEF vuông tại D. Gọi M, N, P lần lượt là trung điểm của DE, DF, EF.
a) Chứng minh tứ giác MNFE là hình thang.
b) Chứng minh tứ giác DMPN là hình chữ nhật.
Hướng dẫn giải
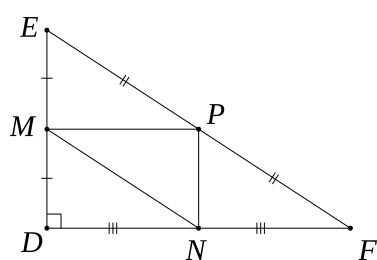
a) Xét tam giác DEF có:
M là trung điểm của DE
N là trung điểm của DF
⇒ MN là đường trung bình của tam giác DEF.
⇒ MN//EF, \(MN = \frac{1}{2}EF\)
⇒ MNFE là hình thang.
b) Xét tam giác DEF có:
M là trung điểm của DE
P là trung điểm của EF
⇒ MP là đường trung bình ΔDEF
⇒ MP//DF, \[MP = \frac{1}{2}DF\]
Lại có: N là trung điểm của DF
\[ \Rightarrow MP = DN = NF = \frac{1}{2}DF\]
Xét tứ giác DMPN có
MP = DN và MP//DN
⇒ DMPN là hình bình hành
Lại có: \[\widehat {EDF} = 90^\circ \]
⇒ DMPN là hình chữ nhật.
Câu 5:
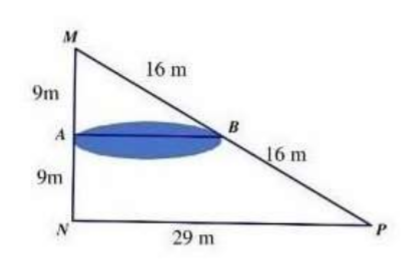
Hướng dẫn giải
∆MNP có:
A là trung điểm của MN (AM = AN = 9m)
B là trung điểm của MP (BM = BP = 16m)
⇒ AB là đường trung bình ΔMNP
\[ \Rightarrow AB = \frac{1}{2}NP = \frac{1}{2}.29 = 14,5\] (m).
