Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 9)
-
2145 lượt thi
-
13 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Đáp án đúng là: A
3x.(2 – 5xy2) = 6x – 15x2y2
Câu 2:
Đáp án đúng là: B
x3– 6x2+ 12x – 8 = x3– 3 . x2. 2 + 3 . x . 22– 23= (x – 2)3
Câu 3:
Đáp án đúng là: D
A = x2– 10x + 26
= x2– 10x + 25 + 1
= (x – 5)2+ 1
Thay x =15 vào A ta được:
A = (15 – 5)2+ 1 = 101.
Câu 4:
Đáp án đúng là: D
(a + b)2– (a – b)2
= (a + b – a + b)(a + b + a – b)
= 2b.2a
= 4ab
Câu 5:
Đáp án đúng là: B
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Câu 6:
Đáp án đúng là: C
Vì ABCD là tứ giác, ta có: \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \)
\( \Rightarrow \widehat D = 360^\circ - 120^\circ - 80^\circ - 100^\circ = 60^\circ \)
Câu 7:
Đáp án đúng là: B
Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
Câu 8:
Biểu thức (2x – 3)(4x2+ 6x + 9) bằng biểu thức:
Đáp án đúng là: C
(2x – 3)(4x2+ 6x + 9) = (2x)3– 33= 8x3– 27
Câu 9:
a) Rút gọn biểu thức A = (x – 3)(x2+ 3x + 9) + x2(2 – x).
b) Cho biểu thức: B = x2– 4 – (x + 2)(x – 1). Tính giá trị biểu thức B với x = –1.
Hướng dẫn giải
a) A = (x – 3)(x2+ 3x + 9) + x2(2 – x)
= x3– 27 + 2x2– x3
= 2x2 – 27
b) B = x2– 4 – (x + 2)(x – 1)
= (x – 2)(x + 2) – (x + 2)(x – 1)
= (x + 2).(–1)
Với x = –1 ta có: B = (–1 + 2).(–1) = 1.
Câu 10:
a) x3– 4x2;
b) 3x2+ 5y – 3xy – 5x ;
c) x2+ 10x + 25 – 4y2.
Hướng dẫn giải
a) x3– 4x2= x2(x – 4)
b) 3x2+ 5y – 3xy – 5x
= 3x(x – y) – 5(x – y)
= (x – y)(3x – 5)
c) x2+ 10x + 25 – 4y2
= (x + 5)2– 4y2
= (x + 5 + 2y)(x + 5 – 2y)
Câu 11:
a) 3(x – 2) + 4 = 0;
b) x2– 6x + 9 = 0;
c) x2– 3x + 2 = 0.
Hướng dẫn giải
a) 3(x – 2) + 4 = 0
\[ \Leftrightarrow x--2 = - {\rm{ }}\frac{4}{3}\;\]
\[ \Leftrightarrow x = \frac{2}{3}\]
Vậy \[x = \frac{2}{3}\].
b) x2– 6x + 9 = 0
⇔ (x – 3)2= 0
⇔ x – 3 = 0
⇔ x = 3
Vậy x = 3.
c) x2– 3x + 2 = 0
⇔ x2– 2x – x + 2 = 0
⇔ (x – 2)(x – 1) = 0
\( \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\x - 1 = 0\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\)
Vậy x = 2 và x = 1.
Câu 12:
a) Chứng minh: Tứ giác AMCN là hình bình hành.
b) Trên thì BC lấy điểm I sao cho: CI = BC Chứng mình: AC = DI.
c) Gọi O là giao điểm của AC và MN. Chứng minh: NO là đường trung bình của ΔACD.
d) Chứng minh: MC // NI.
Hướng dẫn giải
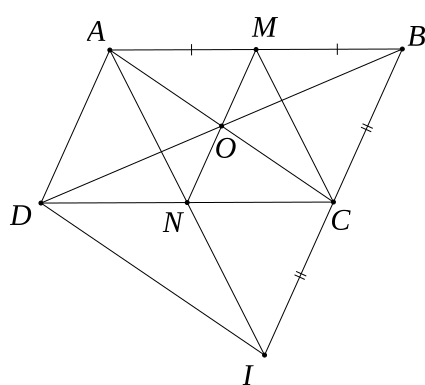
a) Ta có ABCD là hình bình hành (gt)
⇒ AB // CD; AB = CD; AD // BC; AD = BC
Mà M thuộc AB, N thuộc DC ⇒ AM // NC
Xét tứ giác AMCN có:
AM // NC (chứng minh trên)
AN // MC (giả thiết)
⇒ Tứ giác AMCN là hình bình hành.
b) AD // BC; I thuộc BC
⇒ AD // CI
Vì AD = BC (cmt); CI = BC (gt)
⇒ AD = CI
Xét tứ giác ACID có:
AD // CI (cmt)
AD = CI (cmt)
⇒ tứ giác ACID là hình bình hành
⇒ AC = DI.
c) AMCN là hình bình hành
⇒ AM = NC; O là trung điểm của AC
mà \[AM = \frac{1}{2}AB\] (M là trung điểm AB); AB = CD (cmt)
\[ \Rightarrow NC = \frac{1}{2}CD\]
⇒ N là trung điểm của CD
Xét ΔACD có:
O là trung điểm của AC (cmt)
N là trung điểm của CD (cmt)
⇒ NO là đường trung bình của ΔACD.
d) Tứ giác ACID có:
AC = DI
AD // CI
⇒ ACID là hình bình hành
Có N là trung điểm của CD
⇒ N là trung điểm AI
⇒ AN = NI, I thuộc AN
Ta có: MC // AN (AMCN là hình bình hành); I thuộc AN
⇒ MC // NI.
Câu 13:
Hướng dẫn giải
A = 4 + 8y2− y4
= − (y4− 8y2+ 16) + 20
= − (y2−4)2+ 20
Do (y2 − 4)2≥ 0 với mọi y
⇔ − (y2 − 4)2≤ 0 với mọi y
⇔ − (y2 − 4)2+ 20 ≤ 20 với mọi y
Dấu " = " xảy ra khi y2− 4 = 0 ⇒ y = ±2
Vậy giá trị lớn nhất của biểu thức A = 20 khi y = ± 2.
