Đề kiểm tra giữa kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề số 9
-
1690 lượt thi
-
5 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Giải các phương trình sau:
a) 3(x – 5) + 2(x + 7) = x + 11.
b) x2 – 4 + 3x(x + 2) = 0.
c) x2 + 3x – 18 = 0.
d)
a) 3(x – 5) + 2(x + 7) = x + 11
Û 3x – 15 + 2x + 14 = x + 11
Û 5x – 1 = x + 11
Û 5x – x = 11 + 1
Û 4x = 12
Û x = 3
Vậy tập nghiệm của phương trình là S = {3}.b) x2 – 4 + 3x(x + 2) = 0
Û (x – 2). (x + 2) + 3x(x + 2) = 0
Û (x + 2). [(x – 2) + 3x] = 0
Û (x + 2). (4x – 2) = 0
Vậy tập nghiệm của phương trình là .
c) x2 + 3x – 18 = 0
Û x2 – 3x + 6x – 18 = 0
Û (x2 – 3x) + (6x – 18) = 0
Û x (x – 3) + 6(x – 3) = 0
Û (x – 3)(x + 6) = 0
Vậy tập nghiệm của phương trình là S = {– 6; 3}.
d)
ĐKXĐ:
Khi đó phương trình đã cho trở thành:
=> (x – 3)(2x – 3) + (x – 5)(–2 – x) – 10 = 2(x + 2)(x – 3)
Û 2x2 – 9x + 9 – x2 + 10 + 3x – 10 = 2(x2 – x – 6)
Û x2 – 6x + 9 = 2x2 – 2x – 12
Û 2x2 – x2 – 2x + 6x – 12 – 9 = 0
Û x2 + 4x – 21 = 0
Û x2 + 7x – 3x – 21 = 0
Û (x2 + 7x) – (3x + 21) = 0
Û x(x + 7) – 3(x + 7) = 0
Û (x + 7)(x – 3) = 0
Vậy tập nghiệm của phương trình là S = {– 7; 3}.
Câu 2:
Giải bài toán bằng cách lập phương trình
Trong đợt dịch Covid tháng 2 – 2021, một siêu thị đã thu mua rau giúp nông dân tỉnh Hải Dương để bán cho người tiêu dùng. Lúc đầu siêu thị dự định bán hết khối lượng rau đó trong vòng 18 ngày. Nhưng thực tế, số lượng người đến mua rau nhiều hơn dự định, vì vậy mỗi ngày siêu thị bán vượt mức 120 kg và đã bán hết khối lượng rau đó sớm hơn dự định 3 ngày. Tính khối lượng rau mà siêu thị đã thu mua.Gọi x (kg) là khối lượng rau mà siêu thị đã thu mua (x > 0)
Theo dự định, khối lượng rau mỗi ngày bán được là: (kg)
Khối lượng rau đó sớm hơn dự định 3 ngày so với dự định nên số theo thực tế số lượng rau đó bán được là: 18 – 3 = 15 (kg)
Thực tế, số rau bán trong 15 ngày nên khối lượng rau mỗi ngày bán được là: (kg)
Theo đề bài, mỗi ngày siêu thị bán vượt mức 120 kg ta có phương trình:
– = 120
x = 10 800 (thỏa mãn)
Vậy khối lượng rau mà siêu thị đã thu mua là 10 800 (kg)
Câu 3:
Cho phương trình ẩn x (với m là tham số)
m2x + 4m – 3 = m2 + x (1)
a) Giải phương trình với m = 2.
b) Tìm các giá trị của m để phương trình (1) có nghiệm duy nhất.
c) Tìm các giá trị nguyên của m để phương trình (1) có nghiệm duy nhất là số nguyên.a) Thay m = 2 vào phương trình (1), ta được:
22x + 4m – 3 = 22 + x
Û 4x + 8 – 3 = 4 + x
Û 4x + 5 = 4 + x
Û 4x – x = 4 – 5
Û 3x = – 1
Û x = – .
Vậy với m = 2 thì phương trình có một nghiệm là x = – .b) Ta có: m2x + 4m – 3 = m2 + x
<=> (m2 – 1)x = m2 – 4m + 3
<=> x =
Để phương trình (1) có một nghiệm duy nhất thì:
m2 – 1 ≠ 0
Û (m + 1)(m – 1) ≠ 0
Û m ≠ ±1.
Vậy để phương trình (1) có một nghiệm duy nhất thì m ≠ ±1.c) Từ câu b ta có: x =
Để phương trình (1) có nghiệm duy nhất là số nguyên thì và m ≠ ±1.
Khi đó, m ≠ ±1 và (m + 1) Î Ư(4) = {±1; ±2; ±4}.
Ta có bảng sau:
Câu 4:
Cho tam giác ABC có ba góc nhọn, các đường cao BD và CE cắt nhau ở H.
a) Chứng minh DABD DACE.
b) Chứng minh CH. CE = CD. CA.
c) Kẻ EK ^ AC tại K; DI ^ EC tại I. Chứng minh AH // IK.
d) Chứng minh SEIK ≤ SABC.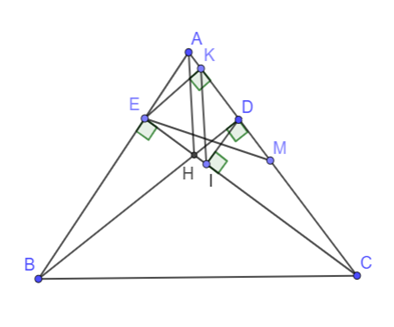
a) Vì BD và CE là đường cao của DABC nên BD ^ AC, CE ^ AB.
Suy ra
Do đó .
Xét DABD và DACE có:
chung
(chứng minh trên)
Do đó DABD DACE (g.g).b) Xét DACE và DHCD có:
= 90° (vì BD ^ AC, CE ^ AB)
chung
Do đó D ACE D HCD (g.g)
Suy ra
Do đó CH. CE = CD. CA (đpcm).c) Xét DCDI và DCEK có:
= 90° (vì EK ^ AC tại K; DI ^ EC tại I)
chung
Do đó D CDI D CEK (g.g)
Suy ra
Theo câu b có: suy ra
Khi đó
Do đó KI // AH (theo định lý Ta-let đảo).
Câu 5:
Cho hai số thực khác nhau a, b thỏa mãn:
Tính giá trị của biểu thức: M =(b – a). (ab2 + a) − (b − a). (a2b + b) = 0
(b – a). (ab2 − a2b + a − b) = 0
(b – a). [ab. (b – a) – (b – a)] = 0
(b – a). (b – a). (ab – 1) = 0
Vì a ≠ b nên b – a ≠ 0
Do đó (b – a). (b – a). (ab – 1) = 0
ab – 1 = 0
ab = 1
a =
