10 câu hỏi trắc nghiệm thuộc Đề kiểm tra giữa kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề số 3

Câu 1:

Tập nghiệm của phương trình x² – x = 0 là:

A. {0}

B. {0; 1}

C. {1}

D. Một kết quả khác.

Xem đáp án

Đáp án B

Ta có: x² – x = 0

$\Leftrightarrow$ x(x – 1) = 0

$\Leftrightarrow$ x = 0 hoặc x – 1 = 0

$\Leftrightarrow$ x = 0 hoặc x = 1.

Vậy tập nghiệm của phương trình đã cho là S = {0; 1}.

Câu 2:

Điều kiện xác định của phương trình

2 + \frac{1}{x - 3} = \frac{5}{x + 3}

là:

A. x ¹ 3

B. x ¹ −3

C. x ¹ 0 và x ¹ 3

D. x ¹ −3 và x ¹ 3.

Xem đáp án

Điều kiện xác định : ${\begin{cases} x - 3 \neq 0 \\ x + 3 \neq 0 \end{cases} \Leftrightarrow {\begin{cases} x \neq 3 \\ x \neq - 3 \end{cases}$

Vậy chọn D.

Câu 3:

Phương trình nào tương đương với phương trình x(x − 2) = x(x − 3) ?

A. x – 2 = x – 3

B. x(x – 2) = 0

C. x = 0

D. (x – 2)( x − 3) = 0

Xem đáp án

Ta có :

+) x(x − 2) = x(x − 3)

$\Leftrightarrow$ x(x − 2) − x(x − 3) = 0

$\Leftrightarrow$ x[(x – 2) – (x − 3)] = 0

$\Leftrightarrow$ x(x – 2 – x + 3) = 0

$\Leftrightarrow$ x = 0.

Do đó phương trình x(x − 2) = x(x − 3) có tập nghiệm S = {0}.

+) x – 2 = x – 3

$\Leftrightarrow$ x – 2 – x + 3 = 0

$\Leftrightarrow$ 1 = 0 (vô lý)

Do đó phương trình x – 2 = x – 3 vô nghiệm.

+) (x – 2)( x − 3) = 0

$\Leftrightarrow$ x – 2 = 0 hoặc x − 3 = 0

$\Leftrightarrow$ x = 2 hoặc x = 3.

Do đó phương trình (x – 2)( x − 3) = 0 có tập nghiệm S = {2 ; 3}.

Vậy chọn C.

Câu 4:

Cho AB = 3 m, CD = 40 cm. Tỉ số của hai đoạn thẳng AB và CD bằng?

A. $\frac{3}{40}$

B.

\frac{40}{3}

C.

\frac{2}{15}

D.

\frac{15}{2}

Xem đáp án

Đổi AB = 3 m = 300 cm.

Tỉ số đoạn thẳng AB và CD là: $\frac{A B}{C D} = \frac{300}{40} = \frac{15}{2}$ .

Đáp án D

Câu 5:

Trong hình vẽ, biết EF // BC, theo định lí Ta-lét thì tỉ lệ thức nào sau đây là đúng?

Trong hình vẽ, biết EF // BC, theo định lí Ta-lét thì tỉ lệ thức nào sau đây là đúng? (ảnh 1)

A. $\frac{B C}{E F} = \frac{A C}{A B}$

B. $\frac{A E}{E C} = \frac{A F}{F B}$

C. $\frac{A F}{A E} = \frac{E F}{B C}$

D. $\frac{A F}{A B} = \frac{E F}{B C}$

Xem đáp án

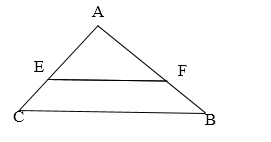
∆ABC, EF // BC. Áp dụng định lý Ta-let, ta được:

$\frac{A E}{E C} = \frac{A F}{F B}$ ; $\frac{A E}{A C} = \frac{A F}{A B} = \frac{E F}{B C}$ .

Vậy chọn B.

Câu 6:

Nếu tam giác ABC đồng dạng k tam giác A’B’C’ theo tỉ số đồng dạng k thì tam giác A’B’C’ đồng dạng tam giácABC theo tỉ số:

A. $\frac{1}{k}$

B. 1

C. k

D. k²

Xem đáp án

DABC DA’B’C’ theo tỉ số đồng dạng k.

Hay $\frac{A B}{A' B'} = k$ .

Do đó DA’B’C’DABC theo tỉ số đồng dạng $\frac{A' B'}{A B} = \frac{1}{k}$ .

Vậy chọn A.

Câu 7:

Giải phương trình:

a) x(x − 3) + 2(x − 3) = 0

b) $\frac{x - 1}{2} + \frac{x - 1}{3} + \frac{x - 1}{2016} = 0$

c) $\frac{3 x + 1}{x + 1} - \frac{2 x - 5}{x - 3} + \frac{7}{x^{2} - 2 x - 3} = 1$ .

Xem đáp án

a) x(x − 3) + 2(x − 3) = 0

$\Leftrightarrow$ (x − 3)(x + 2) = 0

$\Leftrightarrow$ x – 3 = 0 hoặc x + 2 = 0

$\Leftrightarrow$ x = 3 hoặc x = – 2.

Vậy tập nghiệm của phương trình là S = {3; – 2}.

b) $\frac{x - 1}{2} + \frac{x - 1}{3} + \frac{x - 1}{2016} = 0$

$\Leftrightarrow (x - 1) (\frac{1}{2} + \frac{1}{3} + \frac{1}{2016}) = 0$

$\Leftrightarrow$ x – 1 = 0 (vì $\frac{1}{2} + \frac{1}{3} + \frac{1}{2016} > 0$ )

$\Leftrightarrow$ x = 1.

Vậy tập nghiệm của phương trình là S = {1}.

c) $\frac{3 x + 1}{x + 1} - \frac{2 x - 5}{x - 3} + \frac{7}{x^{2} - 2 x - 3} = 1$ .

ĐKXĐ: ${\begin{cases} x + 1 \neq 0 \\ x - 3 \neq 0 \\ x^{2} - 2 x - 3 \neq 0 \end{cases} \Leftrightarrow {\begin{cases} x + 1 \neq 0 \\ x - 3 \neq 0 \\ (x + 1) (x - 3) \neq 0 \end{cases} \Leftrightarrow {\begin{cases} x + 1 \neq 0 \\ x - 3 \neq 0 \end{cases} \Leftrightarrow {\begin{cases} x \neq - 1 \\ x \neq 3 \end{cases}$

Phương trình đã cho tương đương:

$\frac{3 x + 1}{x + 1} - \frac{2 x - 5}{x - 3} + \frac{7}{(x + 1) (x - 3)} = 1$

$\Leftrightarrow \frac{(3 x + 1) (x - 3)}{(x + 1) (x - 3)} - \frac{(2 x - 5) (x + 1)}{(x + 1) (x - 3)} + \frac{7}{(x + 1) (x - 3)} = \frac{(x + 1) (x - 3)}{(x + 1) (x - 3)}$

$\Leftrightarrow$ (3x + 1)(x – 3) – (2x – 5)(x + 1) + 7 = (x + 1)(x – 3)

$\Leftrightarrow$ (3x + 1)(x – 3) – (x + 1)(x – 3) – (2x – 5)(x + 1) + 7 = 0

$\Leftrightarrow$ (3x + 1 – x – 1)(x – 3) – (2x – 5)(x + 1) + 7 = 0

$\Leftrightarrow$ 2x(x – 3) – (2x – 5)(x + 1) + 7 = 0

$\Leftrightarrow$ 2x² – 6x – 2x² – 3x – 5 + 7 = 0

$\Leftrightarrow$ 3x + 2 = 0

$\Leftrightarrow$ 3x = – 2

$\Leftrightarrow x = - \frac{2}{3}$ (TMĐK).

Vậy tập nghiệm của phương trình đã cho là $S = {- \frac{2}{3}}$ .

Câu 8:

Theo kế hoạch hai tổ sản xuất phải làm 900 sản phẩm. Do cải tiến kỹ thuật nên tổ I vượt mức 20% và tổ II vượt mức 15% so với kế hoạch. Vì vậy hai tổ đã sản xuất được 1055 sản phẩm. Hỏi theo kế hoạch mỗi tổ sản xuất được bao nhiêu sản phẩm?

Xem đáp án

Gọi số sản phẩm tổ I sản xuất theo kế hoạch là x (sản phẩm); $(x \in ℕ *, x < 900)$ .

Theo kế hoạch hai tổ sản xuất phải làm 900 sản phẩm.

Khi đó, số sản phẩm tổ II sản xuất theo kế hoạch là 900 – x (sản phẩm).

Thực tế số sản phẩm tổ I sản xuất là:

(100% + 20%).x = 120%.x = $\frac{6}{5} x$ (sản phẩm).

Thực tế số sản phẩm tổ II sản xuất là:

(100% + 15%)(900 − x) = 115%.(900 − x) = $\frac{23}{20} (900 - x)$ (sản phẩm).

Theo đề bài, ta có phương trình:

$\frac{6}{5} x + \frac{23}{20} (900 - x) = 1055$

$\Leftrightarrow \frac{6}{5} x + 1035 - \frac{23}{20} x = 1055$

$\Leftrightarrow \frac{6}{5} x - \frac{23}{20} x = 1055 - 1035$

$\Leftrightarrow$ x = 400 (TMĐK).

Khi đó, tổ II sản xuất được: 900 – x = 900 – 400 = 500 (sản phẩm).

Câu 9:

Cho ΔABC có AB = 8cm, AC = 12cm. Trên cạnh AB lấy điểm D sao cho BD = 2cm, trên cạnh AC lấy điểm E sao cho AE = 9cm.

a) Tính các tỉ số $\frac{AE}{AD}; \frac{AD}{AC}$ .

b) Chứng minh: ΔADE đồng dạng ΔABC.

c) Đường phân giác của $\hat{BAC}$ cắt BC tại I. Chứng minh: IB.AE = IC.AD.

Xem đáp án

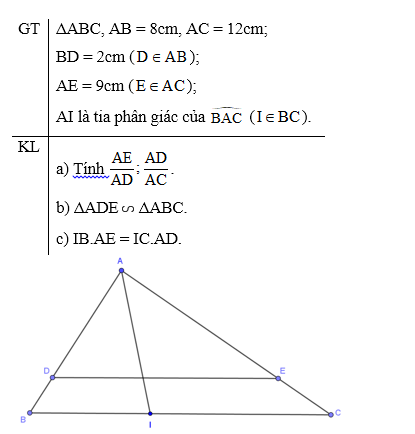
a) Ta có: AD = AB – BD = 8 – 2 = 6 (cm).

Khi đó, $\frac{A E}{A D} = \frac{9}{6} = \frac{3}{2}; \frac{A D}{A C} = \frac{6}{12} = \frac{1}{2}$ .

Vậy $\frac{A E}{A D} = \frac{3}{2}; \frac{A D}{A C} = \frac{1}{2}$ .

b) Ta có $\frac{A D}{A B} = \frac{6}{8} = \frac{3}{4}$ ; $\frac{A E}{A C} = \frac{9}{12} = \frac{3}{4}$ .

Suy ra $\frac{A D}{A B} = \frac{A E}{A C}$ .

Xét ΔADE và ΔABC có:

$\frac{A D}{A B} = \frac{A E}{A C}$ (cmt)

$\hat{D A E}$ chung.

Nên ΔADE ΔABC (c.g.c)

c) AI là tia phân giác của $\hat{B A C}$ , áp dụng tính chất tia phân giác, ta có:

$\frac{I B}{I C} = \frac{A B}{A C}$

Mà $\frac{A D}{A B} = \frac{A E}{A C} \Rightarrow \frac{A B}{A C} = \frac{A D}{A E}$ .

Do đó $\frac{I B}{I C} = \frac{A D}{A E}$ .

Vậy IB.AE = IC.AD (đpcm).

Câu 10:

Giải phương trình sau: 6x⁴ – 5x³ – 38x² – 5x + 6 = 0.

Xem đáp án

6x⁴ – 5x³ – 38x² – 5x + 6 = 0 (1)

* Xét x = 0 thì 6.0⁴ – 5.0³ – 38.0² – 5.0 + 6 = 6 ≠ 0.

Do đó x = 0 không phải là nghiệm của phương trình (1).

* Xét x ≠ 0: chia cả hai vế của phương trình (1) cho x², ta được:

$6 x^{2} - 5 x - 38 - \frac{5}{x} + \frac{6}{x^{2}} = 0$

$\Leftrightarrow (6 x^{2} + \frac{6}{x^{2}}) - (5 x + \frac{5}{x}) - 38 = 0$

$\Leftrightarrow 6 (x^{2} + \frac{1}{x^{2}}) - 5 (x + \frac{1}{x}) - 38 = 0$ (2)

Đặt $t = x + \frac{1}{x}$ $\Rightarrow t^{2} = {(x + \frac{1}{x})}^{2} = x^{2} + \frac{1}{x^{2}} + 2 \Rightarrow t^{2} = {(x + \frac{1}{x})}^{2} = x^{2} + \frac{1}{x^{2}} + 2$

$\Rightarrow x^{2} + \frac{1}{x^{2}} = t^{2} - 2$ .

Khi đó, phương trình (2) tương đương:

6(t² – 2) – 5t – 38 = 0

$\Leftrightarrow$ 6t² – 12 – 5t – 38 = 0

$\Leftrightarrow$ 6t² – 5t – 50 = 0

$\Leftrightarrow$ 6t² + 15t – 20t – 50 = 0

$\Leftrightarrow$ (6t² + 15t) – (20t + 50) = 0

$\Leftrightarrow$ 3t(2t + 5) – 10(2t + 5) = 0

$\Leftrightarrow$ (2t + 5) (3t – 10) = 0

$\Leftrightarrow$ 2t + 5 = 0 hoặc 3t – 10 = 0

$\Leftrightarrow t = - \frac{5}{2}$ hoặc $t = \frac{10}{3}$ .

+) Với $t = - \frac{5}{2}$ thì $x + \frac{1}{x} = - \frac{5}{2}$ $\Leftrightarrow x + \frac{5}{2} + \frac{1}{x} = 0$

$\Leftrightarrow$ 2x² + 5x + 2 = 0

$\Leftrightarrow$ 2x² + 4x + x + 2 = 0

$\Leftrightarrow$ 2x(x + 2) + (x + 2) = 0

$\Leftrightarrow$ (x + 2) (2x + 1) = 0

$\Leftrightarrow$ x + 2 = 0 hoặc 2x + 1 = 0

$\Leftrightarrow$ x = – 2 (TM) hoặc $x = - \frac{1}{2}$ (TM).

Do đó x = – 2; $x = - \frac{1}{2}$ là nghiệm của phương trình (1).

+) Với $t = \frac{10}{3}$ thì $x + \frac{1}{x} = \frac{10}{3}$ $\Leftrightarrow x - \frac{10}{3} + \frac{1}{x} = 0$

$\Leftrightarrow$ 3x² – 10x + 3 = 0

$\Leftrightarrow$ 3x² – 9x – x + 3 = 0

$\Leftrightarrow$ 3x(x – 3) – (x – 3) = 0

$\Leftrightarrow$ (x – 3)(3x – 1) = 0

$\Leftrightarrow$ x – 3 = 0 hoặc 3x – 1 = 0

$\Leftrightarrow$ x = 3 hoặc $x = \frac{1}{3}$ .

Do đó x = 3; $x = \frac{1}{3}$ là nghiệm của phương trình (1).

Vậy tập nghiệm của phương trình (1) là $S = {2; - \frac{1}{2}; 3; \frac{1}{3}}$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra giữa kì 2 Toán 8 có đáp án ( Mới nhất)

Đề kiểm tra giữa kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề số 3

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương