Đề kiểm tra giữa kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề số 11
-
1582 lượt thi
-
16 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Đáp án đúng là: B
Phương trình có dạng ax + b = 0, với a và b là hai số đã cho và a ≠ 0, được gọi là phương trình bậc nhất một ẩn.
Đáp án A sai vì x là mẫu số nên số mũ – 1 không ở dạng bậc nhất.
Đáp án B đúng, phương trình bậc nhất với hệ số và hệ số b = 3.
Đáp án C sai vì phương trình x + y = 0 có có chứa 2 ẩn số x và y nên đây không phải là phương trình bậc nhất một ẩn.
Đáp án D sai vì phương trình 0.x + 1= 0 có hệ số a = 0 nên đây không phải phương trình bậc nhất một ẩn.Câu 2:
Phương án A:
–2,5x = 10
Û x = 10 : (–2,5)
Û x = – 4
Phương trình đã cho có nghiệm là x = – 4;
Phương án B:
–2,5x = –10
Û x = –10 : (–2,5)
Û x = 4
Phương trình đã cho có nghiệm x = 4;
Phương án C:
3x – 8 = 0
Û 3x = 8
Û x =
Phương trình đã cho có nghiệm là x = ;
Phương án D:
3x – 1 = x + 7
Û 3x – x = 7 + 1
Û 2x = 8
Û x = 4
Phương trình đã cho có nghiệm là x = 4.Câu 3:
Đáp án đúng là: C
Ta có:
Vậy tập nghiệm của phương trình đã cho là .
Câu 4:
Đáp án đúng là: B
Gọi số tự nhiên cần tìm có dạng là = 10a + b.
Theo đề, số hàng chục là 3 nên số cần tìm là .
Mà số hàng đơn vị gấp đôi chữ số hàng chục nên ta có phương trình:
b = 2.a = 2.3 = 6.
Vậy số tự nhiên cần tìm là 36.Câu 5:
Đáp án đúng là: B
Giải phương trình đã cho như sau:
2x – 5 = 7
Û 2x = 7 + 5
Û 2x = 12
Û x = 12 : 2
Û x = 6
Vậy nghiệm của phương trình đã cho là x = 6.Câu 6:
Đáp án đúng là: C
Vì |x2| ≥ 0 ∀ x Î ℝ nên x ≥ 0.
Khi đó |x2| = x2 = x
Û x2 – x = 0
Û x(x – 1) = 0
Vậy tập nghiệm của phương trình đã cho là S = {0; 1}.
Câu 7:
Đáp án đúng là: D
Theo đề bài, quãng đường đi từ nhà Bình An đến trường là 7 km.
Bình An đi xe đạp với vận tốc x (km/h).
Thời gian Bình An đi đạp từ nhà đến trường là: (giờ).Câu 8:
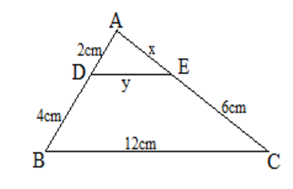
Đáp án đúng là: C
Áp dụng định lý Ta – let trong ∆ABC có DE // BC, D Î AB, E Î AC có:
Suy ra (cm).
Vậy x = 3 cm.Câu 9:
Đáp án đúng là: B
Theo đề ta có AB = AD + BD = 2 + 4 = 6 (cm);
Áp dụng định lý Ta – let trong ∆ABC có DE // BC, D Î AB, E Î AC có:
Suy ra (cm).
Vậy y = 4 cm.Câu 10:
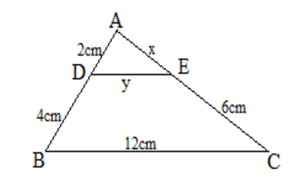
Đáp án đúng là: D
Áp dụng định lý Ta – let trong ∆ABC có DE // BC, D Î AB, E Î AC có:
Xét ∆ADE và ∆ABC có:
chung (gt)
(gt)
Do đó ∆ADE ∆ABC (c.g.c).Câu 11:
Đáp án đúng là: A
Vì ∆A’B’C ∆ABC và có tỉ số đồng dạng bằng (gt)
Suy ra .Câu 12:
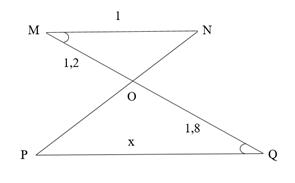
Đáp án đúng là: B
Ta có (hình vẽ) mà hai góc này ở vị trí so le trong
Suy ra MN // PQ.
Áp dụng hệ quả định lý Ta – let có MN // PQ có:
Vậy x = 1,5.
Câu 13:
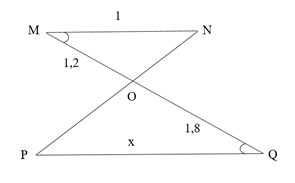
Đáp án đúng là: B
Xét ∆QPO và ∆MNO có:
(gt)
(cmt)
Do đó ∆QPO ∆MNO (c.g.c) theo tỉ số đồng dạng .
Do đó .
Vậy .Câu 14:
Giải các phương trình sau:
a) 7 + 2x = 22 – 3x;
b) (x – 2)(2x + 5) = 0;
c) .a) 7 + 2x = 22 – 3x
Û 2x + 3x = 22 – 7
Û 5x = 15
Û x = 15 : 5
Û x = 3
Vậy nghiệm của phương trình là x =3;b) (x – 2)(2x + 5) = 0;
Vậy tập nghiệm của phương trình đã cho là ;
c)
Vì nên
Suy ra hay .
Do đó phương trình đã cho tương đương với:
x + 1 = Û x = – 1.
Vậy nghiệm của phương trình đã cho là S = { – 1}.Câu 15:
Giải bài toán sau bằng cách lập phương trình.
Một ôtô đi từ A đến B với vận tốc 60 km/h và quay từ B về A với vận tốc 40 km/h.
Tính quãng đường AB. Biết thời gian cả đi lẫn về là 7 giờ 30 phút.Gọi x (km) là độ dài quãng đường AB (x > 0).
Ô tô đi từ A đến B với vận tốc 60 km/h, nên thời gian ô tô đi từ A đến B là h.
Ô tô từ B về A với vận tốc 40 km/h, nên thời gian ô tô đi từ B đến A là h.
Đổi 7 giờ 30 phút = giờ.
Tổng thời gian cả đi lẫn về là 7 giờ 30 phút nên ta có phương trình sau:
Û 2x + 3x = 15.60
Û 5x = 15.60
Û 5x = 5.3.60
Û x = 180 (thỏa mãn)
Vậy quãng đường AB dài 180 km.Câu 16:
Cho tam giác ABC vuông tại A và có đường cao AH.
a) Chứng minh ∆HBA đồng dạng ∆ABC.
b) Cho biết AB = 6cm, AC = 8cm. Hãy tính độ dài BC, AH, BH và CH?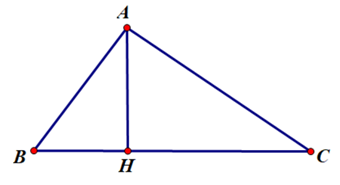
a) Xét ∆HBA và ∆ABC có:
chung
(vì AH là đường cao của ∆ABC)
Do đó ∆HBA ∆ABC (g.g).b) Áp dụng định lý Py-ta-go trong ∆ABC vuông tại A có:
BC2 = AB2 + AC2 = 62 + 82 = 100
Suy ra BC = 10 cm.
Ta có ∆ABC vuông tại A. Khi đó diện tích tam giác ABC là:
SABC = AB.AC = .6.8 = 24 (cm2)
Mặc khác, ∆ABC có AH là đường cao kẻ từ A ứng với cạnh BC nên ta có:
SABC = AH.BC = 24
(cm)
Xét ∆HBA vuông tại H, áp dụng định lý Py-ta-go, ta có:
AB2 = AH2 + HB2
Suy ra HB2 = AB2 – AH2 = 62 – 4,82 = 12,96.
Do đó HB = 3,6 cm.
Ta có: BC = BH + CH
Suy ra CH = BC – BH = 10 – 3,6 = 6,4 (cm).
Vậy độ dài BC, AH, BH và CH lần lượt là: 10 cm; 4,8 cm; 3,6 cm và 6,4 cm.