Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 5
-
2038 lượt thi
-
13 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Thực hiện phép tính:
Phương pháp:
Sử dụng quy tắc nhân đơn, đa thức với đa thức và bảy hằng đẳng thức đáng nhớ:
Cách giải:
Câu 2:
Thực hiện phép tính:
Phương pháp:
Sử dụng quy tắc nhân đơn, đa thức với đa thức và bảy hằng đẳng thức đáng nhớ:
Cách giải:
Câu 3:
Thực hiện phép tính:
Phương pháp:
Sử dụng quy tắc nhân đơn, đa thức với đa thức và bảy hằng đẳng thức đáng nhớ:
Cách giải:
Câu 4:
Phân tích đa thức thành nhân tử:
Phương pháp:
Sử dụng các phương pháp phân tích đa thức thành nhân tử, bảy hằng đẳng thức đáng nhớ.
Cách giải:
Câu 5:
Phân tích đa thức thành nhân tử:
Phương pháp:
Sử dụng các phương pháp phân tích đa thức thành nhân tử, bảy hằng đẳng thức đáng nhớ.
Cách giải:
Câu 6:
Phân tích đa thức thành nhân tử:
Phương pháp:
Sử dụng các phương pháp phân tích đa thức thành nhân tử, bảy hằng đẳng thức đáng nhớ.
Cách giải:
Câu 8:
Chỉ số khối cơ thể - thường được biết đến với chữ viết tắt BMI theo tên tiếng Anh Body Mass Index - được dùng để đánh giá mức độ gầy hay béo của một người. Chỉ số này do nhà bác học người Bỉ Adolphe Quetelet đưa ra năm 1832.
Gọi W là khối lượng của một người (tính bằng kg) và H là chiều cao của người đó (tính bằng mét), chỉ số khối cơ thể BMI được tính theo công thức:
Anh Nam cao 170 cm và cân nặng là 85kg. Dựa vào thông tin trên và bảng phân loại bên, em hãy tính chỉ số BMI của anh Nam và cho biết phân loại tình trạng dinh dưỡng ở mức nào?
|
Phương pháp:
Áp dụng công thức tính chỉ số BMI:
Cách giải:
Đổi
Chỉ số BMI của anh Nam là:
Anh Nam ở mức béo phì độ I.
Câu 9:
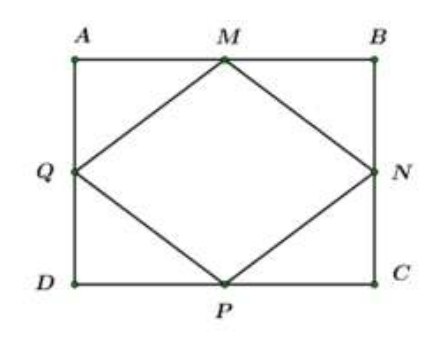
Một nền nhà hình chữ nhật ABCD có chiều dài 6,4 mét và chiều rộng 4,8 mét, người ta dự định trải lên nền nhà này một tấm thảm hình thoi có 4 đỉnh lần lượt là trung điểm M, N, P, Q của các cạnh hình chữ nhật ABCD. Tính cạnh của tấm thảm hình thoi đó.
Phương pháp:
Sử dụng định lý Pitago.
Cách giải:
Giả sử
Tấm thảm có dạng như hình vẽ trên.
Vì M là trung điểm của AB
Q là trung điểm của AD
Áp dụng định lý Pitago cho vuông tại A ta có:
Vậy cạnh của tấm thảm hình thoi là 4m
Câu 10:
Cho hình chữ nhật ABCD. Gọi E là điểm đối xứng của B qua C.
Chứng minh tứ giác ACED là hình bình hành.
Phương pháp:
Dựa vào tính chất, dấu hiệu nhận biết hình bình hành, hình thoi.
Cách giải:
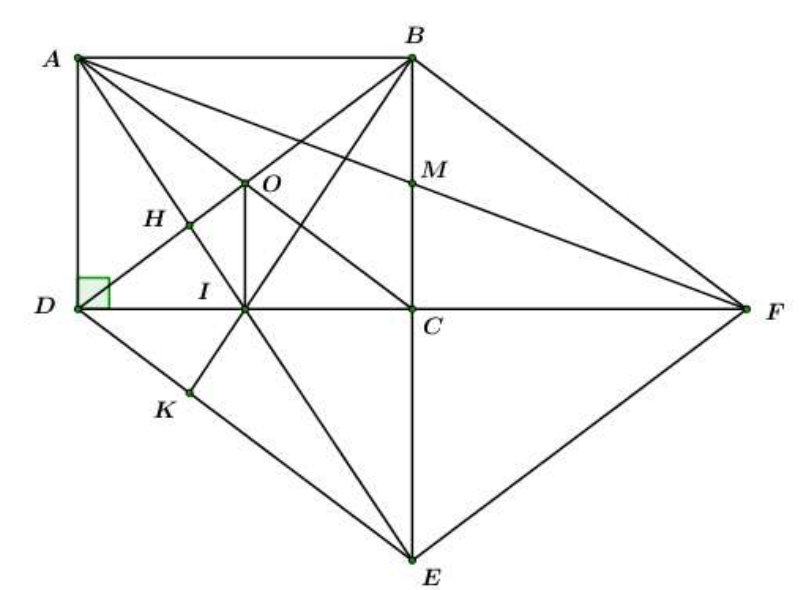
Chứng minh tứ giác ACED là hình bình hành.
Ta có: E là điểm đối xứng với B qua C.
C là trung điểm của BE
Xét tứ giác ACED ta có:
ACED là hình bình hành. (dhnb)
Câu 11:
Cho hình chữ nhật ABCD. Gọi E là điểm đối xứng của B qua C.
Gọi M là trung điểm của BC. Tia AM cắt tia DC tại F. Chứng minh tứ giác BDEF là hình thoi.
Phương pháp:
Dựa vào tính chất, dấu hiệu nhận biết hình bình hành, hình thoi.
Cách giải:
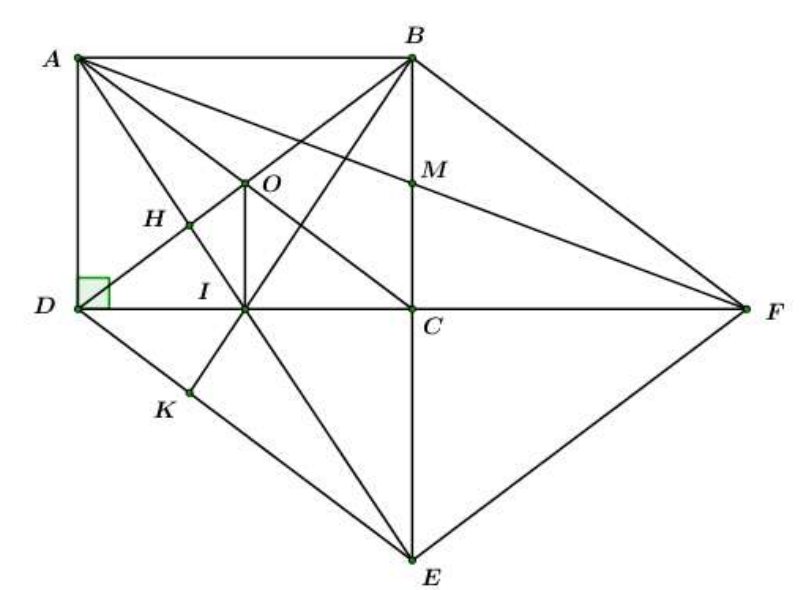
Gọi M là trung điểm của BC. Tia AM cắt tia DC tại F. Chứng minh tứ giác BDEF là hình thoi.
Xét và ta có:
(hai góc đối đỉnh)
(g – c – g)
(hai cạnh tương ứng).
Mà
Xét tứ giác BDEF ta có:
C là trung điểm của BE, DF
BDEF là hình thoi. (hình thoi có 2 đường chéo vuông góc với nhau tại trung điểm của mỗi đường).
Câu 12:
Cho hình chữ nhật ABCD. Gọi E là điểm đối xứng của B qua C.
Gọi I là giao điểm của AE và DC. Tia BI cắt DE tại K. Chứng minh
Phương pháp:
Dựa vào tính chất, dấu hiệu nhận biết hình bình hành, hình thoi.
Cách giải:
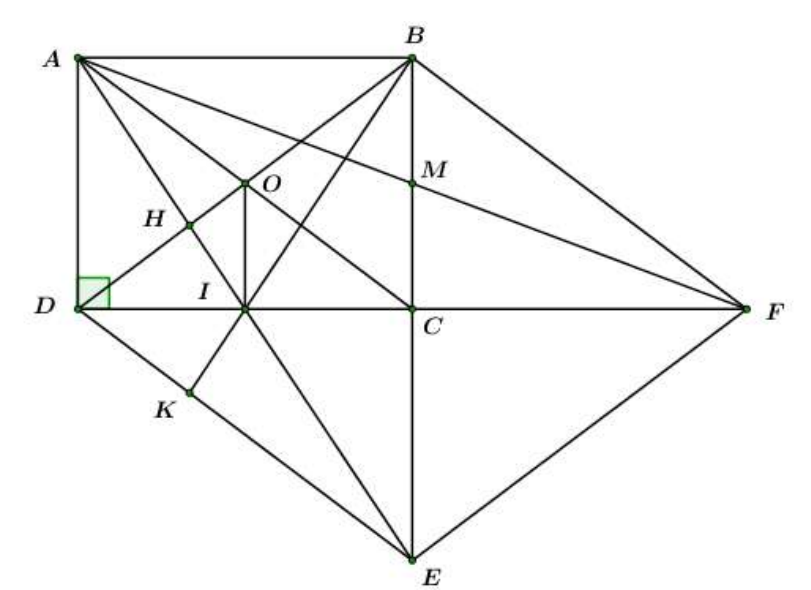
Gọi I là giao điểm của AE và DC. Tia BI cắt DE tại K. Chứng minh .
Gọi
Ta có: ACED là hình bình hành (cmt).
Mà I là trung điểm của CD.
Lại có: O là trung điểm của AC
H là trực tâm của
Mà I là trung điểm của AE
Ta có: BDEF là hình thoi (cmt)
DF là tia phân giác của (tính chất hình thoi).
Ta có: BDEF là hình thoi (cmt) (hai cạnh bên).
Xét và ta có:
DI chung
(c – g – c).
(hai góc tương ứng).
Và (hai cạnh tương ứng).
Xét và ta có:
(hai góc đối đỉnh)
(g – c – g).
Câu 13:
Chứng minh rằng với n là số tự nhiên và
Phương pháp:
Dựa vào quy tắc nhân đa thức với đa thức và công thức:
Cách giải:
Ta có:
Vậy với mọi
