13 câu hỏi trắc nghiệm thuộc Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 14

Câu 1:

Phân tích các đa thức sau thành nhân tử: $5 x^{2} y^{3} - 25 x^{3} y^{4} + 10 x^{3} y^{3}$

Phương pháp:

Phương pháp đặt nhân tử chung, tìm ra ước chung và chọn chúng làm nhân tử.

Cách giải:

$5 x^{2} y^{3} - 25 x^{3} y^{4} + 10 x^{3} y^{3} = 5 x^{2} y^{3} .1 - 5 x^{2} y^{3} .5. x . y + 5 x^{2} y^{3} .2. x$

$= 5 x^{2} y^{3} (1 - 5 x y + 2 x)$

Câu 2:

Phân tích các đa thức sau thành nhân tử: $x y - 3 x - 2 y + 6$

Xem đáp án

Phương pháp:

Phương pháp nhóm nhiều hạng tử.

Cách giải:

$x y - 3 x - 2 y + 6 = (x y - 3 x) + (- 2 y + 6)$

$= x (y - 3) - 2 (y - 3)$

$= (y - 3) (x - 2)$

Câu 3:

Phân tích các đa thức sau thành nhân tử: $x^{2} - 6 x y - 4 z^{2} + 9 y^{2}$

Xem đáp án

Phương pháp:

Phương pháp nhóm nhiều hạng tử kết hợp với dùng hằng đẳng thức.

Cách giải:

$(x^{2} - 6 x y - 4 z^{2} + 9 y^{2}) - 4 z^{2}$

$= [x^{2} - 2. x .3 y + {(3 y)}^{2}] - {(2 z)}^{2}$

$= {(x - 3 y)}^{2} - {(2 z)}^{2}$

$= (x - 3 y + 2 z) (x - 3 y - 2 z)$

Câu 4:

Rút gọn các biểu thức sau: ${(x - 2)}^{2} - {(2 x - 1)}^{2} + (3 x - 1) (x - 5)$

Xem đáp án

Phương pháp:

Khai triển hằng đẳng thức ${(x - 2)}^{2}; {(2 x - 1)}^{2}$ và nhân 2 đa thức $(3 x - 1) (x - 5)$ sau đó phá ngoặc và rút gọn đa thức.

Cách giải:

${(x - 2)}^{2} - {(2 x - 1)}^{2} + (3 x - 1) (x - 5)$

$= x^{2} - 4 x + 4 - 4 x^{2} + 4 x - 1 + 3 x^{2} - 15 x - x + 5$

$= (x^{2} - 4 x^{2} + 3 x^{2}) + (- 4 x + 4 x - 15 x - x) + (4 - 1 + 5)$

$= - 16 x + 8$

Câu 5:

Rút gọn các biểu thức sau: ${(x - 3)}^{3} - (x + 3) (x^{2} - 3 x + 9) + (3 x - 1) (3 x + 1)$

Xem đáp án

Phương pháp:

Khai triển hằng đẳng thức ${(x - 3)}^{2}$ ; áp dụng hằng đẳng thức hiệu hai lập phương và hiệu hai bình phương để nhân 2 đa thức $(x + 3) (x^{2} - 3 x + 9)$ và 2 đa thức $(3 x - 1) (3 x + 1)$ ; sau đó phá ngoặc và rút gọn đa thức.

Cách giải:

${(x - 3)}^{3} - (x + 3) (x^{2} - 3 x + 9) + (3 x - 1) (3 x + 1)$

$= (x^{3} - 3. x^{2} .3 + 3. x {.3}^{2} - 3^{3}) - (x + 3) (x^{2} - 3. x + 3^{2}) + [{(3 x)}^{2} - 1^{2}]$

$= x^{3} - 9 x^{2} + 27 x - 27 - (x^{3} + 3^{3}) + 9 x^{2} - 1$

$= x^{3} - 9 x^{2} + 27 x - 27 - x^{3} - 27 + 9 x^{2} - 1$

$= (x^{3} - x^{3}) + (- 9 x^{2} + 9 x^{2}) + 27 x + (- 27 - 27 - 1)$

$= 27 x - 55$

Câu 6:

Tìm x: ${(x + 3)}^{2} - x . (x + 5) = 2$

Xem đáp án

Phương pháp:

Rút gọn vế trái.

Cách giải:

${(x + 3)}^{2} - x . (x + 5) = 2$

$\Leftrightarrow (x^{2} + 6 x + 9) + (- x^{2} - 5 x) = 2$

$\Leftrightarrow x^{2} + 6 x + 9 - x^{2} - 5 x = 2$

$\Leftrightarrow x + 9 = 2$

$\Leftrightarrow x = 2 - 9$

$\Leftrightarrow x = - 7$

Câu 7:

Tìm x: ${(5 x - 2)}^{2} + (2 - 5 x) (3 x + 1) = 0$

Xem đáp án

Phương pháp:

Phân tích vế trái thành nhân tử chung.

Cách giải:

${(5 x - 2)}^{2} + (2 - 5 x) (3 x + 1) = 0 \Leftrightarrow {(5 x - 2)}^{2} - (5 x - 2) (3 x + 1) = 0$

$\Leftrightarrow (5 x - 2) [(5 x - 2) - (3 x + 1)] = 0$

$\Leftrightarrow (5 x - 2) (5 x - 2 - 3 x - 1) = 0 \Leftrightarrow (5 x - 2) (2 x - 3) = 0$

$\Leftrightarrow [\begin{array}{l} 5 x - 2 = 0 \\ 2 x - 3 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{2}{5} \\ x = \frac{3}{2} \end{array}$

Câu 8:

Tìm x: $x^{3} + 27 + (x + 3) (x - 9) = 0$

Xem đáp án

Phương pháp:

Phân tích vế trái thành nhân tử chung.

Cách giải:

$x^{3} + 27 + (x + 3) (x - 9) = 0$

$\Leftrightarrow (x^{3} + 3^{3}) + (x + 3) (x - 9) = 0$

$\Leftrightarrow (x + 3) (x^{2} - 3 x + 9) + (x + 3) (x - 9) = 0$

$\Leftrightarrow (x + 3) (x^{2} - 3 x + 9 + x - 9) = 0$

$\Leftrightarrow (x + 3) (x^{2} - 2. x) = 0 \Leftrightarrow x (x + 3) (x - 2) = 0 \Leftrightarrow [\begin{array}{l} x = 0 \\ x + 3 = 0 \\ x - 2 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = 0 \\ x = - 3 \\ x = 2 \end{array}$

Câu 9:

Cho $Δ A B C$ là tam giác nhọn, có AM là đường trung tuyến. Trên cạnh AC lấy hai điểm D và E sao cho $A D = D E = E C$ . AM cắt BD tại I.

Chứng minh: tứ giác BDEM là hình thang

Xem đáp án

Phương pháp:

Sử dụng tính chất đường trung bình, tứ giác có 2 cạnh đối song song là hình thang.

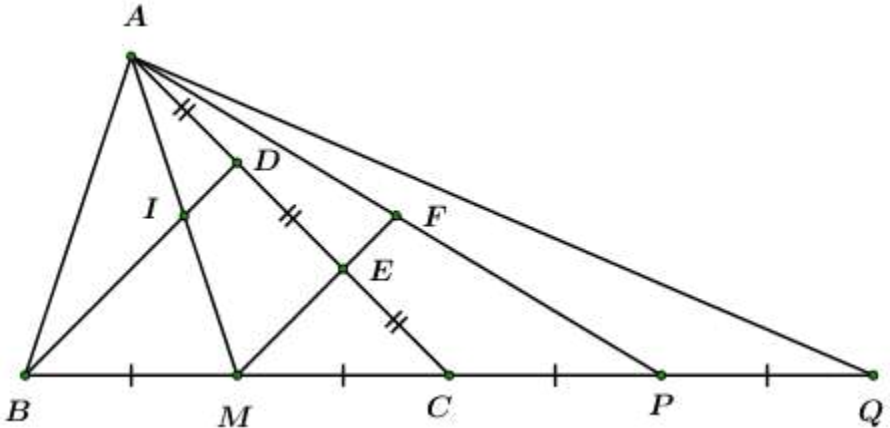
Cách giải:

Xét $Δ C B D$ có M là trung điểm BC, E là trung điểm DC

Þ ME là đường trung bình của $Δ C B D$

$\Rightarrow M E ∥ B D; M E = \frac{1}{2} B D$ (tính chất đường trung bình)

Þ Tứ giác BDEM là hình thang (tứ giác có 2 cạnh đối song song là hình thang)

Câu 10:

Cho

Δ A B C

là tam giác nhọn, có AM là đường trung tuyến. Trên cạnh AC lấy hai điểm D và E sao cho

A D = D E = E C

. AM cắt BD tại I.

Chứng minh: I là trung điểm của AM.

Xem đáp án

Phương pháp:

Sử dụng tính chất bắc cầu.

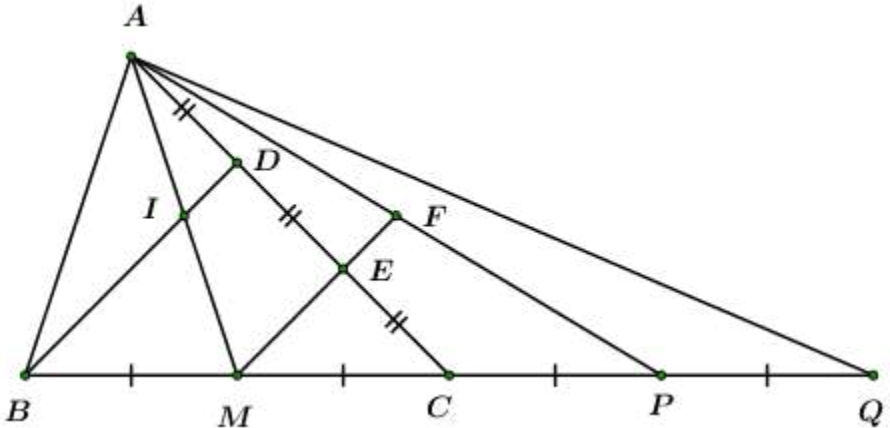
Cách giải:

Ta có: $M E ∥ B D \Rightarrow I D ∥ M E$

Mà: D là trung điểm của AE

Þ I là trung điểm của AM

Câu 11:

Cho

Δ A B C

là tam giác nhọn, có AM là đường trung tuyến. Trên cạnh AC lấy hai điểm D và E sao cho

A D = D E = E C

. AM cắt BD tại I.

Chứng minh: BI= 3DI

Xem đáp án

Phương pháp:

Áp dụng tính chất đường trung bình.

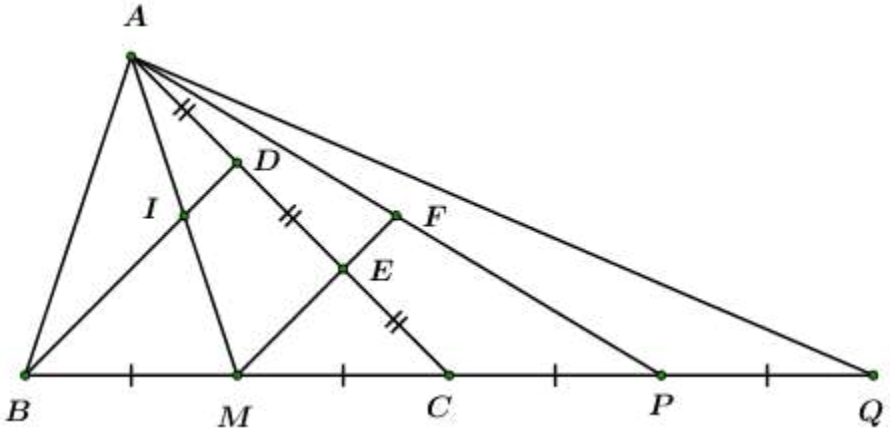
Cách giải:

Ta có: $I D = \frac{1}{2} M E$ (tính chất đường trung bình) $\Rightarrow I D = \frac{1}{2} . \frac{1}{2} B D = \frac{1}{4} B D (M E = \frac{1}{2} B D (c m t))$

$B I = B D - D I = B D - \frac{1}{2} B D = \frac{3}{4} B D$

$\Rightarrow B I = 3 I D$

Câu 12:

Cho

Δ A B C

là tam giác nhọn, có AM là đường trung tuyến. Trên cạnh AC lấy hai điểm D và E sao cho

A D = D E = E C

. AM cắt BD tại I.

Trên tia đối của tia CB lấy hai điểm P và Q sao cho $C P = P Q = C M$ . Chứng minh: ME, AP, DQ đồng quy tại một điểm.

Xem đáp án

Phương pháp:Chứng minh có một điểm đồng thời thuộc cả ba đường thẳng đó. hay F thuộc DQ.

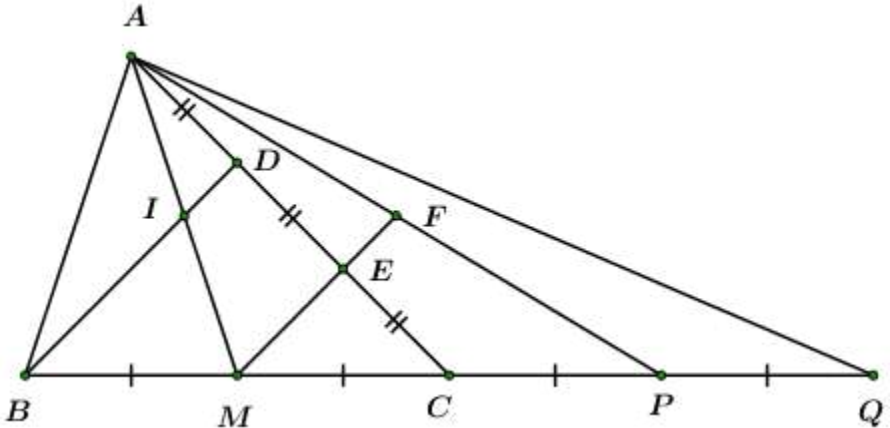
Cách giải:

Gọi $F = M E \cap A P$

Xét $Δ A M P$ có AC là đường trung tuyến, $A E = \frac{2}{3} A C$ Þ E là trọng tâm $Δ A M P$ $\Rightarrow E F = \frac{1}{2} M E$

$E F ∥ I D (d o M E ∥ I D : c m t); I D = E F = \frac{1}{2} M E$

Þ IDFE là hình bình hành (tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành)

$\Rightarrow I E ∥ D F (1)$

Ta có: $B I = \frac{3}{4} B D$ (chứng minh trên); $B P = \frac{3}{4} B Q$

$\Rightarrow I P ∥ D Q$ (định lý Ta-lét đảo trong tam giác)

IP là đường trung tuyến trong $Δ A M P$ $\Rightarrow I P \equiv I E \Rightarrow I E ∥ D Q (2)$

Từ (1) và (2) $\Rightarrow D F \equiv D Q$ hay $F \in D Q$

Vậy ME, DQ, AP đồng quy tại F.

Câu 13:

Tìm giá trị nhỏ nhất của biểu thức sau: $A = 2 x^{2} + 10 y^{2} - 6 x y - 6 x - 2 y + 16$

Xem đáp án

Phương pháp:

Đưa biểu thức về dạng: $A = {[f (x)]}^{2} + a$

Khi đó biểu thức A min khi $f (x) = 0$ và GTNN của A chính bằng a.

Cách giải:

$A = 2 x^{2} + 10 y^{2} - 6 x y - 6 x - 2 y + 16$

$= x^{2} - 6 x y + 9 y^{2} + x^{2} - 6 x + 9 + y^{2} - 2 y + 1 + 6$

$= {(x - 3 y)}^{2} + {(x - 3)}^{2} + {(y - 1)}^{2} + 6$

Ta có: ${(x - 3 y)}^{2} \geq 0; {(x - 3)}^{2} \geq 0; {(y - 1)}^{2} \geq 0$ với mọi x, y

$A \min \Leftrightarrow \{\begin{cases} {(x - 3 y)}^{2} = 0 \\ {(x - 3)}^{2} = 0 \\ {(y - 1)}^{2} = 0 \end{cases} \Leftrightarrow \{\begin{cases} x - 3 y = 0 \\ x - 3 = 0 \\ y - 1 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 y \\ x = 3 \\ y = 1 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 \\ y = 1 \end{cases}$

Vậy GTNN của A là 6 khi $x = 3$ và $y = 1$ .

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bộ 14 đề thi Học kì 1 Toán 8 có đáp án

Bộ 14 đề thi Học kì 1 Toán 8 có đáp án - Đề 14

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương