13 câu hỏi trắc nghiệm thuộc Dạng 4: Giải phương trình dạng lf(x)l = g(x) có đáp án

Câu 1:

Giải phương trình: $|x + 4| + 3 x = 5$

Xem đáp án

Ta có thể lựa chọn một trong hai cách sau:

Cách 1: Xét hai trường hợp:

Trường hợp 1: Nếu $x + 4 \geq 0 \Leftrightarrow x \geq - 4$ . (1)

Khi đó, phương trình có dạng:

$x + 4 + 3 x = 5 \Leftrightarrow 4 x = 1 \Leftrightarrow x = \frac{1}{4}$ , thỏa mãn điều kiện (1).

Trường hợp 2: Nếu $x + 4 < 0 \Leftrightarrow x < - 4$ (2)

Khi đó, phương trình có dạng:

$- (x + 4) + 3 x = 5 \Leftrightarrow 2 x = 9 \Leftrightarrow x = \frac{9}{2}$ , không thỏa mãn (2)

Vậy, phương trình có nghiệm $x = \frac{1}{4}$ .

Cách 2: Viết lại phương trình dưới dạng:

$|x + 4| = 5 - 3 x$ .

Với điều kiện:

$5 - 3 x \geq 0 \Leftrightarrow x \leq \frac{5}{3}$ .

Khi đó, phương trình được biến đổi:

$|x + 4| = 5 - 3 x \Leftrightarrow [\begin{array}{l} x + 4 = 5 - 3 x \\ x + 4 = - (5 - 3 x) \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{1}{4} \\ x = \frac{9}{2} lo¹i \end{array}$

Vậy, phương trình có nghiệm $x = \frac{1}{4}$ .

Câu 2:

Giải các phương trình sau:

$a . |2 x| = x - 6$

Xem đáp án

a. Ta có thể trình bày theo các cách sau:

Cách 1: Ta có:

$|2 x| = [\begin{array}{l} 2 x k h i x \geq 0 \\ - 2 x k h i x < 0 \end{array}$

Xét hai trường hợp:

Trường hợp 1: Nếu $x \geq 0$ phương trình có dạng:

$2 x = x - 6 \Leftrightarrow x = - 6$ , không thỏa mãn điều kiện.

Trường hợp 2: Nếu $x < 0$ phương trình có dạng:

$- 2 x = x - 6 \Leftrightarrow 3 x = 6 \Leftrightarrow x = 2$ , không thỏa mãn điều kiện.

Vậy, phương trình vô nghiệm.

Cách 2: Với điều kiện:

$x - 6 \geq 0 \Leftrightarrow x \geq 6$ (*)

Khi đó, phương trình được biến đổi:

$[\begin{array}{l} 2 x = x - 6 \\ 2 x = - (x - 6) \end{array} \Leftrightarrow [\begin{array}{l} x = - 6 \\ 3 x = 6 \end{array} \Leftrightarrow [\begin{array}{l} x = - 6 \\ x = 2 \end{array}$ , không thỏa mãn (*).

Vậy, phương trình vô nghiệm.

Câu 3:

$b . |4 x| = 2 x + 12$

Xem đáp án

b. Ta có thể trình bày theo các cách sau:

Cách 1: Ta có:

$|4 x| = [\begin{array}{l} 4 x k h i x \geq 0 \\ - 4 x k h i x < 0 \end{array}$

Xét hai trường hợp:

Trường hợp 1: Nếu $x \geq 0$ phương trình có dạng:

$4 x = 2 x + 12 \Leftrightarrow x = 6$ , (thỏa mãn).

Trường hợp 2: Nếu x < 0 phương trình có dạng:

$- 4 x = 2 x + 12 \Leftrightarrow x = - 2$ , (thỏa mãn).

Vậy, phương trình có hai nghiệm x = 6 và x = -2.

Cách 2: Với điều kiện:

$2 x + 12 \geq 0 \Leftrightarrow x \geq - 6$ (*)

Khi đó, phương trình được biến đổi:

$[\begin{array}{l} 4 x = 2 x + 12 \\ 4 x = - (2 x + 12) \end{array} \Leftrightarrow [\begin{array}{l} 2 x = 12 \\ 6 x = - 12 \end{array} \Leftrightarrow [\begin{array}{l} x = 6 \\ x = - 2 \end{array}$ , thỏa mãn (*).

Vậy, phương trình có hai nghiệm x = 6 và x = -2.

Câu 4:

$c . |- 3 x| = x - 8$

Xem đáp án

c. Viết lại phương trình dưới dạng:

$|3 x| = x - 8$

Ta có thể trình bày theo các cách sau:

Cách 1: Ta có:

$|3 x| = [\begin{array}{l} 3 x k h i x \geq 0 \\ - 3 x k h i x < 0 \end{array}$

Xét hai trường hợp:

Trường hợp 1: Nếu $x \geq 0$ phương trình có dạng:

$3 x = x - 8 \Leftrightarrow 2 x = - 8 \Leftrightarrow x = - 4$ , không thỏa mãn điều kiện.

Trường hợp 2: Nếu x < 0 phương trình có dạng:

$- 3 x = x - 8 \Leftrightarrow 4 x = 8 \Leftrightarrow x = 2$ , không thỏa mãn điều kiện.

Vậy, phương trình vô nghiệm.

Cách 2: Với điều kiện:

$x - 8 \geq 0 \Leftrightarrow x \geq 8$ (*)

Khi đó, phương trình được biến đổi:

$[\begin{array}{l} 3 x = x - 8 \\ 3 x = - (x - 8) \end{array} \Leftrightarrow [\begin{array}{l} 2 x = - 8 \\ 4 x = 8 \end{array} \Leftrightarrow [\begin{array}{l} x = - 4 \\ x = 2 \end{array}$ , không thỏa mãn (*).

Vậy, phương trình vô nghiệm.

Câu 5:

$d . |- 5 x| - 16 = 3 x$

Xem đáp án

d. Viết lại phương trình dưới dạng:

$|5 x| = 3 x + 16$

Ta có thể trình bày theo các cách sau:

Cách 1: Ta có:

$|5 x| = [\begin{array}{l} 5 x k h i x \geq 0 \\ - 5 x k h i x < 0 \end{array}$

Xét hai trường hợp:

Trường hợp 1: Nếu $x \geq 0$ phương trình có dạng:

$5 x = 3 x + 16 \Leftrightarrow 2 x = 16 \Leftrightarrow x = 8$ , thỏa mãn điều kiện.

Trường hợp 2: Nếu x < 0 phương trình có dạng:

$- 5 x = 3 x + 16 \Leftrightarrow 8 x = - 16 \Leftrightarrow x = - 2$ , thỏa mãn điều kiện.

Vậy, phương có hai nghiệm x = 8 và x = -2.

Cách 2: Với điều kiện:

$3 x + 16 \geq 0 \Leftrightarrow x \geq - \frac{16}{3}$ (*)

Khi đó, phương trình được biến đổi:

$[\begin{array}{l} 5 x = 3 x + 16 \\ 5 x = - (3 x + 16) \end{array} \Leftrightarrow [\begin{array}{l} 2 x = 16 \\ 8 x = - 16 \end{array} \Leftrightarrow [\begin{array}{l} x = 8 \\ x = - 2 \end{array}$ , thỏa mãn (*).

Vậy, phương có hai nghiệm x = 8 và x = -2.

Câu 6:

Giải các phương trình sau:

$a . |x - 7| = 2 x + 3$

Xem đáp án

a. Ta có thể trình bày theo các cách sau:

Cách 1: Ta có:

$|x - 7| = [\begin{array}{l} x - 7 k h i x \geq 7 \\ - x + 7 k h i x < 7 \end{array}$

Xét hai trường hợp:

Trường hợp 1: Nếu $x \geq 7$ phương trình có dạng:

$x - 7 = 2 x + 3 \Leftrightarrow x = - 10$ , không thỏa mãn điều kiện.

Trường hợp 2: Nếu x < 7 phương trình có dạng:

$- x + 7 = 2 x + 3 \Leftrightarrow 3 x = 4 \Leftrightarrow x = \frac{4}{3}$ , thỏa mãn điều kiện.

Vậy, phương có nghiệm $x = \frac{4}{3}$ .

Cách 2: Với điều kiện:

$2 x + 3 \geq 0 \Leftrightarrow x \geq - \frac{3}{2}$ (*)

Khi đó, phương trình được biến đổi:

$[\begin{array}{l} x - 7 = 2 x + 3 \\ x - 7 = - (2 x + 3) \end{array} \Leftrightarrow [\begin{array}{l} x = - 10 \\ 3 x = 4 \end{array} \Leftrightarrow [\begin{array}{l} x = - 10 (loại) \\ x = \frac{4}{3} \end{array}$

Vậy, phương có nghiệm $x = \frac{4}{3}$ .

Câu 7:

$b . |x + 4| = 2 x - 5$

Xem đáp án

b. Ta có thể trình bày theo các cách sau:

Cách 1: Ta có:

$|x + 4| = [\begin{array}{l} x + 4 k h i x \geq - 4 \\ - x - 4 k h i x < - 4 \end{array}$

Xét hai trường hợp:

Trường hợp 1: Nếu $x \geq - 4$ phương trình có dạng:

$x + 4 = 2 x - 5 \Leftrightarrow x = 9$ , thỏa mãn điều kiện.

Trường hợp 2: Nếu x < -4 phương trình có dạng:

$- x - 4 = 2 x - 5 \Leftrightarrow 3 x = 1 \Leftrightarrow x = \frac{1}{3}$ , không thỏa mãn điều kiện.

Vậy, phương có nghiệm x = 9.

Cách 2: Với điều kiện:

$2 x - 5 \geq 0 \Leftrightarrow x \geq \frac{5}{2}$ (*)

Khi đó, phương trình được biến đổi:

$[\begin{array}{l} x + 4 = 2 x - 5 \\ x + 4 = - (2 x - 5) \end{array} \Leftrightarrow [\begin{array}{l} x = 9 \\ 3 x = 1 \end{array} \Leftrightarrow [\begin{array}{l} x = 9 \\ x = \frac{1}{3} (lo¹i) \end{array}$

Vậy, phương có nghiệm x = 9.

Câu 8:

$c . |x + 3| = 3 x - 1$

Xem đáp án

c. Ta có thể trình bày theo các cách sau:

Cách 1: Ta có:

$|x + 3| = [\begin{array}{l} x + 3 k h i x \geq - 3 \\ - x - 3 k h i x < - 3 \end{array}$

Xét hai trường hợp:

Trường hợp 1: Nếu $x \geq - 3$ phương trình có dạng:

$x + 3 = 3 x - 1 \Leftrightarrow 2 x = 4 \Leftrightarrow x = 2$ , thỏa mãn điều kiện.

Trường hợp 2: Nếu x < -3 phương trình có dạng:

$- x - 3 = 3 x - 1 \Leftrightarrow 4 x = - 2 \Leftrightarrow x = - \frac{1}{2}$ , không thỏa mãn điều kiện.

Vậy, phương có nghiệm x = 2.

Cách 2: Với điều kiện:

$3 x - 1 \geq 0 \Leftrightarrow x \geq \frac{1}{3}$ (*)

Khi đó, phương trình được biến đổi:

$[\begin{array}{l} x + 3 = 3 x - 1 \\ x + 3 = - (3 x - 1) \end{array} \Leftrightarrow [\begin{array}{l} 2 x = 4 \\ 4 x = - 2 \end{array} \Leftrightarrow [\begin{array}{l} x = 2 \\ x = - \frac{1}{2} (loại) \end{array}$

Vậy, phương có nghiệm x = 2.

Câu 9:

$d . |x - 4| + 3 x = 5$

Xem đáp án

d. Viết lại phương trình dưới dạng:

$|x - 4| = 5 - 3 x$ .

Ta có thể trình bày theo các cách sau:

Cách 1: Ta có:

$|x - 4| = [\begin{array}{l} x - 4 k h i x \geq 4 \\ - x + 4 k h i x < 4 \end{array}$

Xét hai trường hợp:

Trường hợp 1: Nếu $x \geq 4$ phương trình có dạng:

$x - 4 = 5 - 3 x \Leftrightarrow 4 x = 9 \Leftrightarrow x = \frac{9}{4}$ , không thỏa mãn điều kiện.

Trường hợp 2: Nếu x < 4 phương trình có dạng:

$- x + 4 = 5 - 3 x \Leftrightarrow 2 x = 1 \Leftrightarrow x = \frac{1}{2}$ , thỏa mãn điều kiện.

Vậy, phương có nghiệm $x = \frac{1}{2}$ .

Cách 2: Với điều kiện:

$5 - 3 x \geq 0 \Leftrightarrow x \leq \frac{5}{3}$ (*)

Khi đó, phương trình được biến đổi:

$[\begin{array}{l} x - 4 = 5 - 3 x \\ x - 4 = - (5 - 3 x) \end{array} \Leftrightarrow [\begin{array}{l} 4 x = 9 \\ 2 x = 1 \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{9}{4} (l o ạ i) \\ x = \frac{1}{2} \end{array}$

Vậy, phương có nghiệm $x = \frac{1}{2}$ .

Câu 10:

Giải các phương trình:

$a . |x + 1| = x^{2} + x$

Xem đáp án

a. Xét hai trường hợp:

Trường hợp 1: Nếu $x + 1 \geq 0 \Leftrightarrow x \geq - 1$ (1)

Khi đó, phương trình có dạng:

$x + 1 = x^{2} + x \Leftrightarrow x^{2} = 1$

$\Leftrightarrow x = \pm 1$ , thỏa mãn điều kiện (1).

Trường hợp 2: Nếu $x + 1 < 0 \Leftrightarrow x < - 1$ (2)

Khi đó, phương trình có dạng:

$- (x + 1) = x^{2} + x \Leftrightarrow x^{2} + 2 x + 1 = 0 \Leftrightarrow {(x + 1)}^{2} = 0$

$\Leftrightarrow x = - 1$ , không thỏa mãn điều kiện (2).

Vậy, phương trình có hai nghiệm $x = \pm 1$

Câu 11:

$b . |x^{2} - 2 x| + 4 = 2 x$

Xem đáp án

b. Viết lại phương trình dưới dạng:

$|x^{2} - 2 x| = 2 x - 4$ .

Với điều kiện:

$2 x - 4 \geq 0 \Leftrightarrow x \geq 2$ (*)

Khi đó, phương trình được biến đổi:

$|x^{2} - 2 x| = 2 x - 4 \Leftrightarrow [\begin{array}{l} x^{2} - 2 x = 2 x - 4 \\ x^{2} - 2 x = - (2 x - 4) \end{array} \Leftrightarrow [\begin{array}{l} x^{2} - 4 x + 4 = 0 \\ x^{2} = 4 \end{array}$

$\Leftrightarrow [\begin{array}{l} {(x - 2)}^{2} = 0 \\ x = \pm 2 \end{array} \Leftrightarrow [\begin{array}{l} x = 2 \\ x = - 2 k h ô n g t h o ả m ã n (*) \end{array}$

Vậy, phương trình có nghiệm x =2.

Câu 12:

Giải phương trình: $|x - 1| + |x - 3| = 2$

Xem đáp án

Nhận xét rằng:

$x - 1 \geq 0 \Leftrightarrow x \geq 1 x - 3 \geq 0 \Leftrightarrow x \geq 3$

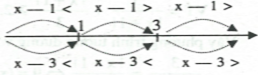
Giải phương trình: trị tuyệt đối x - 1 + trị tuyệt đối x - 3 = 2 (ảnh 1)

Do đó, để thực hiện việc bỏ dấu giá trị tuyệt đối cho phương trình chúng ta cần phải xét ba trường hợp.

Trường hợp 1: Nếu $x \leq 1$ (1)

Khi đó, phương trình có dạng:

$- (x - 1) - (x - 3) = 2 \Leftrightarrow - 2 x + 4 = 2$

<=> x = 1, thỏa mãn điều kiện (1).

Trường hợp 2: Nếu 1 < x < 3 (2)

Khi đó, phương trình có dạng:

$(x - 1) - (x - 3) = 2 \Leftrightarrow 2 = 2$ , luôn đúng.

Trường hợp 3: Nếu $x \geq 3$ (3)

Khi đó, phương trình có dạng:

$(x - 1) + (x - 3) = 2 \Leftrightarrow 2 x - 4 = 2$

<=> x = 3, thỏa mãn điều kiện (3).

Vậy, phương trình có nghiệm $1 \leq x \leq 3$ .

Câu 13:

Giải phương trình:

\frac{3}{|x + 1|} + \frac{|x + 1|}{3} = 2

Xem đáp án

Điều kiện xác định của phương trình là $x \neq - 1$ .

Ta có thể lựa chọn một trong hai cách sau:

Cách 1: Đặt $t = \frac{|x + 1|}{3}$ , điều kiện t > 0.

Khi đó, $(1) \Leftrightarrow \frac{1}{t} + t = 2 \Leftrightarrow t^{2} - 2 t + 1 = 0 \Leftrightarrow t = 1$

$\Leftrightarrow \frac{|x + 1|}{3} = 1 \Leftrightarrow |x + 1| = 3 \Leftrightarrow [\begin{array}{l} x + 1 = 3 \\ x + 1 = - 3 \end{array} \Leftrightarrow [\begin{array}{l} x = 2 \\ x = - 4 \end{array}$

Vậy, phương trình có 2 nghiệm x = 2 và x = -4.

Cách 2: Áp dụng bất đẳng thức Côsi, ta được:

$V T = \frac{3}{|x + 1|} + \frac{|x + 1|}{3} \geq 2. \sqrt{\frac{3}{|x + 1|} . \frac{|x + 1|}{3}} = 2 = V P$

Vậy phương trình tương đương với:

$\frac{3}{|x + 1|} = \frac{|x + 1|}{3} \Leftrightarrow 9 = {(x + 1)}^{2} \Leftrightarrow [\begin{array}{l} x + 1 = 3 \\ x + 1 = - 3 \end{array} \Leftrightarrow [\begin{array}{l} x = 2 \\ x = - 4 \end{array}$

Vậy, phương trình có 2 nghiệm x = 2 và x = -4.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Bài tập Toán 8 Chủ đề 5: Phương trình chứa dấu giá trị tuyệt đối có đáp án

Dạng 4: Giải phương trình dạng lf(x)l = g(x) có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương