Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 22
-
2958 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Giải phương trình
a) 4x – 5 = 2x + 1
Hướng dẫn giải
a) 4x – 5 = 2x + 1
Û 4x – 2x = 5 + 1
Û 2x = 6
Û x = 3
Vậy tập nghiệm của phương trình là S = {3}.
Câu 2:
Giải phương trình
b) 2x(3x - 1) + 6x - 2 = 0
b) 2x(3x - 1) + 6x - 2 = 0
Û 6x2 - 2x + 6x - 2 = 0
Û 6x2 + 4x - 2 = 0
Û 3x2 + 2x - 1 = 0
Û 3x2 + 3x - x - 1 = 0
Û 3x(x + 1) - (x + 1) = 0
Û (3x - 1)(x + 1) = 0
Vậy tập nghiệm của phương trình là
Câu 3:
Giải phương trình
c)
c) ĐKXĐ:
Ta có:
Þ -x - 13 = 1 - 5x
Û -x + 5x = 1 + 13
Û 4x = 14
(thỏa mãn ĐKXĐ).
Vậy tập nghiệm của phương trình là
Câu 4:
Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:
.
Hướng dẫn giải
Û 4(1 - 2x) ³ 9(2 - x)
Û 4 - 8x ³ 18 - 9x
Û 9x - 8x ³ 18 - 4
Û x ³ 14
Vậy tập nghiệm của bất phương trình là S = {x | x ³ 14}
Khi đó biểu diễn tập nghiệm của bất phương trình trên trục số là:

Câu 5:
Một mảnh đất hình chữ nhật có chu vi 100 m và chiều dài hơn chiều rộng 6 m. Tính diện tích của mảnh đất.
Hướng dẫn giải
Gọi a (m) là chiều dài của mảnh đất hình chữ nhật (a > 0)
+) Hình chữ nhật có chu vi 100 (m) nên suy ra tổng chiều dài và chiều rộng của mảnh vườn đó là 100 : 2 = 50 (m)
Khi đó ta có chiều rộng của mảnh vườn là 50 ‒ a (m)
Điều kiện 50 ‒ a > 0 ⇔ a < 50
Vậy điều kiện của a là 0 < a < 50
+) Chiều dài hơn chiều rộng 6 (m) nên suy ra
a - (50 ‒ a) = 6
Hay a – 50 + a = 6
Tương đương 2a = 50 + 6
Hay 2a = 56
Vậy suy ra a = 56 : 2 = 28 (m) (thỏa mãn ĐKXĐ)
Với a = 28 nên suy ra chiều rộng của mảnh vườn là 50 − 28 = 22 (m)
Diện tích của mảnh đất hình chữ nhật là:
28.22 = 616 (m2).
Vậy diện tích của mảnh đất hình chữ nhật là 616 m2.
Câu 6:
Một trạm xăng trong một ngày bán được 1500 lít xăng gồm hai loại là xăng sinh học E5 và xăng A95, thu được 29 598 000 đồng. Nếu giá một lít xăng E5 là 18 500 đồng, giá một lít xăng A95 là 20 180 đồng. Em hãy tìm xem trạm xăng ấy bán bao nhiêu lít xăng mỗi loại.

Hướng dẫn giải
Gọi x (l) là số lít xăng E5 mà tiệm xăng ấy bán được trong một ngày (Với x > 0)
+) Một trạm xăng trong một ngày bán được 1500 lít xăng nên suy ra số lít xăng A95 mà tiệm đấy bán được là 1500 ‒ x (lít)
Điều kiện 1500 ‒ x > 0 ⇔ x < 1500
Vậy điều kiện của x là 0 < x < 1500
+) Một ngày cửa hàng bán được 29 598 000 đồng với giá một lít xăng E5 là 18 500 đồng, giá một lít xăng A95 là 20 180 đồng nên suy ra
Þ 18 500x + 20 180(1500 ‒ x) = 2 9598 000
Û 925x + 1 009(1500 ‒ x) = 1 479 900
Û 925x + 1 513 500 − 1 009x = 1 479 900
Û 1 009x − 925x = 1 513 500 – 1 479 900
Û 84x = 33 600
Û x = 400 (thỏa mãn)
Từ đó ta suy ra được số lít xăng A95 mà trạm đó bán được một ngày là:
1500 ‒ 1100 = 400 (l)
Vậy một ngày trạm xăng đó bán được 400 lít xăng E5 và 1100 lít xăng A95.
Câu 7:
Để hạn chế nguy cơ gãy đổ cây xanh khi mưa gió. Nhóm công nhân thuộc công ty cây xanh Thành phố Hồ Chí Minh đã cắt tỉa gọn các cành trên cây phượng của trường THCS Huỳnh Văn Nghệ. Tại thời điểm đó bóng của thân cây phượng trên sân trường dài 4,2m, còn bóng của một học sinh cao 1,5m đang đứng trên sân trường là 1,25m. Hỏi thân cây phượng cao bao nhiêu mét.
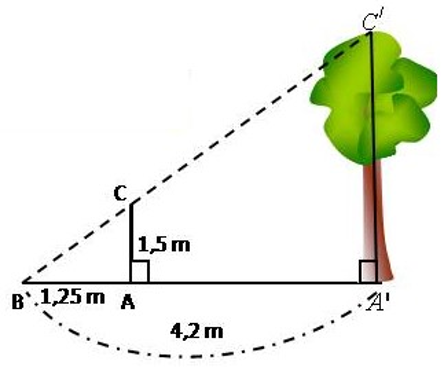
Hướng dẫn giải
Ta có: CA ^ BA' và C'A' ^ BA' nên suy ra CA // C'A'
Áp dụng định lý Ta-lét vào tam giác A'BC' có CA // C'A'
Vậy thân cây phượng đó cao bao nhiêu 5,04 mét.
Câu 8:
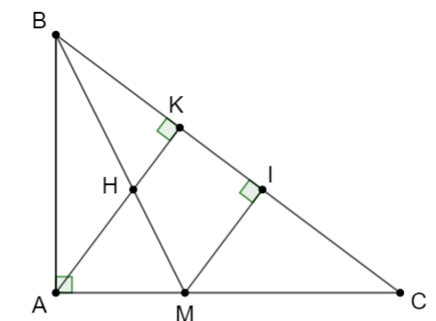
Cho tam giác ABC vuông tại A, đường cao AK, biết AB = 12cm, BC = 20cm.
a) Chứng minh DKBA ᔕ DABC và tính BK.
Hướng dẫn giải
a) Xét hai tam giác DKBA và DABC có:
Câu 9:
b) Chứng minh: AK2 = KB.KC
b) +) Xét DAKB là tam vuông tại K nên suy ra:
(1)
+) Xét DACB là tam giác vuông tại A nên suy ra:
(2)
Từ (1) và (2) suy ra (cùng phụ với góc )
Xét hai tam giác DBKA và DAKC có:
Câu 10:
c) Phân giác của góc ABC cắt AK và AC lần lượt tại H và M. Kẻ MI vuông góc BC (I thuộc BC) Chứng minh
c) Ta có:
+) MI ^ BC và AK ^ BC nên suy ra MI // AK
Áp dụng định lý Ta-lét vào tam giác AKC có MI // AK:
(3)
+) BM là đường phân giác của góc ABC nên suy ra
Theo tính chất đường phân giác
(4)
Từ (3) và (4) ta suy ra được
(đpcm).
