11 câu hỏi trắc nghiệm thuộc Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 14

Câu 1:

Giải các phương trình

a) 8x - 7 = 3x + 23

Xem đáp án

Hướng dẫn giải

a) 8x - 7 = 3x + 23

Û 8x - 3x = 7 + 23

Û 5x = 30

Û x = 6

Vậy tập nghiệm của phương trình là S = {6}.

Câu 2:

Giải các phương trình

b) 3x(x + 2) - 4(x + 2) = 0

Xem đáp án

b) 3x(x + 2) - 4(x + 2) = 0

Û 3x² + 6x - 4x - 8 = 0

Û 3x² + 2x - 8 = 0

Û 3x² + 6x - 4x - 8 = 0

Û 3x(x + 2) - 4(x + 2) = 0

Û (x + 2)(3x - 4) = 0

$\Leftrightarrow [\begin{matrix} x + 2 = 0 \\ 3 x - 4 = 0 \end{matrix}$

\Leftrightarrow [\begin{matrix} x = - 2 \\ x = \frac{4}{3} \end{matrix}

Vậy nghiệm của phương trình là $S = \{- 2; \frac{4}{3}\}$

Câu 3:

Giải các phương trình

c) |4x - 1| = x + 3

Xem đáp án

c) |4x - 1| = x + 3 (1)

+) TH1: x + 3 ³ 0 Û x ³ -3

Phương trình (1) trở thành

Û 4x - 1 = x + 3

Û 4x - x = 3 + 1

Û 3x = 4 (thỏa mãn điều kiện)

+) TH2: x + 3 £ 0 Û x £ -3

Phương trình (1) trở thành

Û 4x - 1 = -x - 3

Û 4x + x = -3 + 1

Û 5x = -2

$\Leftrightarrow x = \frac{- 2}{5}$ (không thỏa mãn)

Vậy nghiệm của phương trình là

x = \frac{4}{3}

Câu 4:

Giải các phương trình

d) $\frac{x - 1}{x - 3} - \frac{1}{x - 3} = \frac{3 x + 3}{x^{2} - 9}$

Xem đáp án

d)

$\frac{x - 1}{x - 3} - \frac{1}{x + 3} = \frac{3 x + 3}{x^{2} - 9}$

$\Leftrightarrow \frac{x - 1}{x - 3} - \frac{1}{x + 3} = \frac{3 x + 3}{(x - 3) (x + 3)}$

ĐKXĐ: $\{\begin{matrix} x - 3 \neq 0 \\ x + 3 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 3 \\ x \neq - 3 \end{matrix}$

Phương trình đã cho trở thành:

$\frac{(x - 1) (x + 3)}{(x - 3) (x + 3)} - \frac{x - 3}{(x - 3) (x + 3)} = \frac{3 x + 3}{(x - 3) (x + 3)}$

$\Leftrightarrow \frac{x^{2} - x + 3 x - 3}{(x - 3) (x + 3)} - \frac{x - 3}{(x - 3) (x + 3)} = \frac{3 x + 3}{(x - 3) (x + 3)}$

$\Leftrightarrow \frac{x^{2} + 2 x - 3}{(x - 3) (x + 3)} - \frac{x - 3}{(x - 3) (x + 3)} = \frac{3 x + 3}{(x - 3) (x + 3)}$

$\Leftrightarrow \frac{x - 1}{x - 3} - \frac{1}{x + 3} = \frac{3 x + 3}{(x - 3) (x + 3)}$

$\Leftrightarrow \frac{x^{2} + x}{(x - 3) (x + 3)} = \frac{3 x + 3}{(x - 3) (x + 3)}$

Þ x² + x = 3x + 3

Û x(x + 1) = 3(x + 1)

$\Leftrightarrow [\begin{matrix} x + 1 = 0 \\ x = 3 \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = - 1 \\ x = 3 \end{matrix}$

Đối chiếu ĐKXĐ suy ra x = -1 là nghiệm của phương trình.

Vậy tập nghiệm của phương trình đã cho là S = {-1}.

Câu 5:

Giải và biểu diễn tập nghiệm của bất phương trình:

a) 6x - 5 > 2x + 3

Xem đáp án

Hướng dẫn giải

a) 6x - 5 > 2x + 3

Û 6x - 2x > 3 + 5

Û 4x > 8

Û x > 2

Vậy tập nghiệm của bất phương trình là S = {x | x > 2}.

Câu 6:

Giải và biểu diễn tập nghiệm của bất phương trình:

b) $\frac{5 x}{2} + \frac{2 x - 3}{7} \leq \frac{3 x + 3}{x^{2} - 9}$

Xem đáp án

b)

$\frac{5 x}{2} + \frac{2 x - 3}{7} \leq \frac{38 x}{14}$

$\Leftrightarrow \frac{35 x}{14} + \frac{2 (2 x - 3)}{14} \leq \frac{38 x}{14}$

$\Leftrightarrow \frac{35 x}{14} + \frac{4 x - 6}{14} \leq \frac{38 x}{14}$

$\Leftrightarrow \frac{35 x + 4 x - 6}{14} \leq \frac{38 x}{14}$

$\Leftrightarrow \frac{39 x - 6}{14} \leq \frac{38 x}{14}$

Û 39x - 6 £ 38x

Û 39x - 38x £ 6

Û x £ 6

Vậy tập nghiệm của bất phương trình là S = {x | x £ 6}.

Câu 7:

Một người đi xe máy từ A đến B với vận tốc 50 km/h và sau đó từ B trở về A với vận tốc là 40 km/h. Do đó thời gian về nhiều hơn thời gian đi là 48 phút. Tĩnh quãng đường AB.

Xem đáp án

Hướng dẫn giải

Gọi x (m) là độ dài quãng đường AB (x > 0)

Một người đi xe máy từ A đến B với vận tốc 50 km/h hết $\frac{x}{50} (h)$

Người đó đi từ B trở về A với vận tốc là 40 km/h hết $\frac{x}{40} (h)$

Đổi: 48 phút = $\frac{4}{5}$ giờ

Do thời gian về nhiều hơn thời gian đi là 48 phút tức nhiều hơn $\frac{4}{5}$ giờ nên ta có phương trình:

$\frac{x}{40} - \frac{x}{50} = \frac{4}{5}$

$\Leftrightarrow \frac{5 x}{200} - \frac{4 x}{200} = \frac{4}{5}$

$\Leftrightarrow \frac{x}{200} = \frac{4}{5}$

$\Leftrightarrow x = \frac{4}{5} .200 = 160$ (TMĐK)

Vậy độ dài quãng đường AB là 160 (km).

Câu 8:

Cho DMNP có ba góc nhọn hai đường cao NI và PK cắt nhau tại H.

a) Chứng minh: DMNI đồng dạng với DMPK.

Xem đáp án

Hướng dẫn giải

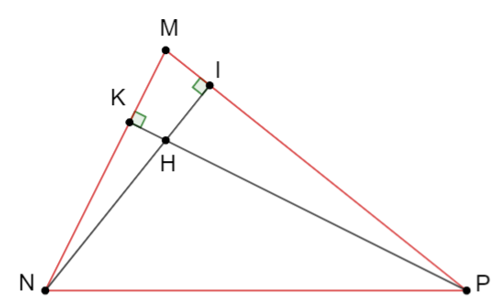
Cho MNP có ba góc nhọn hai đường cao NI và PK cắt nhau tại H. a) Chứng minh: tam giác MNI đồng dạng với tam giác MPK. (ảnh 1)

a) Xét hai tam giác DMNI đồng dạng với DMPK có:

$\begin{matrix} \hat{M I N} = \hat{M K P} (= 90 °) \\ \hat{N M I} = \hat{P M K} (\hat{M} c h u n g) \end{matrix}\} \Rightarrow Δ M N I ∽ Δ M P K (g . g)$

$\Rightarrow \frac{N I}{P K} = \frac{M N}{M P} = \frac{M I}{M K}$

Câu 9:

b) Chứng minh: HN.HI = HK.HP.

Xem đáp án

b) Xét hai tam giác DNHK đồng dạng với DPHI có:

$\begin{matrix} \hat{N K H} = \hat{P I H} (= 90 °) \\ \hat{N H K} = \hat{P H I} \end{matrix}\} \Rightarrow Δ N H K ∽ Δ P H I (g . g)$

$\Rightarrow \frac{N H}{H P} = \frac{H K}{H I} \Leftrightarrow H N . H I = H K . H P$ (đpcm)

Câu 10:

c) Chứng minh: NI.NH + PK.PH = NP².

Xem đáp án

c) Ta có:

NI.NH + PK.PH = NH.(NH + HI) + PK.PH

= NH² + NH.HI + PK.PH

= NH² + HK.HP + PK.PH

= NK² + HK² + HK.HP + HP.(HK + HP)

= NK² + HK² + HK.HP + HP.HK + HP²

= NK² + (HK² + 2HK.HP + HP2)

= NK² + (HK + HP)²

= NK² + PK² = NP² (đpcm, theo định lý Pytago vào ∆NKP vuông tại K).

Câu 11:

Một xe chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước dài cao rộng là 3 m; 1 m; 2 m. Tính thể tích thùng xe.

Xem đáp án

Hướng dẫn giải

Một xe chở hàng có thùng xe dạng hình hộp chữ nhật với kích thước dài cao rộng là 3 m; 1 m; 2 m.

Khi đó, thể tích thùng xe là:

3.2.1 = 6 (m³).

Vậy thể tích thùng xe là 6 m³.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất)

Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 14

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương