14 câu hỏi trắc nghiệm thuộc Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25

Câu 1:

Bất phương trình 2x - 3 > 5 có tập nghiệm biểu diễn bởi hình vẽ nào?

A. Bất phương trình 2x - 3 > 5 có tập nghiệm biểu diễn bởi hình vẽ nào? (ảnh 2)

B.

Bất phương trình 2x - 3 > 5 có tập nghiệm biểu diễn bởi hình vẽ nào? (ảnh 3)

C.

Bất phương trình 2x - 3 > 5 có tập nghiệm biểu diễn bởi hình vẽ nào? (ảnh 4)

D.

Bất phương trình 2x - 3 > 5 có tập nghiệm biểu diễn bởi hình vẽ nào? (ảnh 5)

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

2x - 3 > 5

Û 2x > 5 + 3

Û 2x > 8 Û x > 4

Vậy tập nghiệm của bất phương trình là S = {x | x > 4}.

Khi đó, biểu diễn của tập nghiệm trên trục số là:

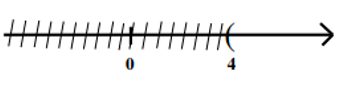
Bất phương trình 2x - 3 > 5 có tập nghiệm biểu diễn bởi hình vẽ nào? (ảnh 1)

Câu 2:

Trong các bất phương trình sau, đâu là bất phương trình bậc nhất một ẩn ?

A. 2x - y > 0;

B. -3x - 2 £ 0;

C. x(x + 2) < 0;

D. 0x + 2 > 0.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

+) 2x - y > 0

Þ Không là bất phương trình bậc nhất một ẩn.

+) -3x - 2 £ 0

Û 3x ³ -2

Þ Đây là bất phương trình bậc nhất một ẩn.

+) x(x + 2) < 0

Û x² + 2x < 0

Þ Đây là bất phương trình bậc hai một ẩn.

+) 0x + 2 > 0

Vì a = 0 nên suy ra đây không là bất phương trình bậc nhất một ẩn.

Câu 3:

Nếu một hình lập phương có cạnh là 5 cm thì thể tích của hình lập phương đó là

A. 125 lít;

B. 25 cm³;

C. 25 cm²;

D. 125 cm³.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Thể tích của hình lập phương có cạnh bằng 5 là:

V = 5³ = 125 (cm³).

Câu 4:

Cho ∆ABC ᔕ ∆DEF, biết AB = 3 cm; DE = 2 cm và diện tích của ∆DEF bằng 6 cm². Diện tích của ∆ABC bằng:

A. 9 cm²;

B. 12 cm²;

C. 13,5 cm²;

D. 15,5 cm².

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Theo đề bài: ∆ABC ᔕ ∆DEF.

Nên suy ra tỉ lệ diện tích hai tam giác bằng bình phương tỉ số đồng dạng

$\Rightarrow \frac{S_{A B C}}{S_{D E F}} = {(\frac{A B}{D E})}^{2}$

$\Leftrightarrow S_{A B C} = S_{D E F} . {(\frac{A B}{D E})}^{2} = 6. {(\frac{3}{2})}^{2} = 13,5 (c m^{2}) .$

Câu 5:

Giải các phương trình và bất phương trình sau:

a) 4x - 13 = x - 1;

Xem đáp án

Hướng dẫn giải

a) 4x - 13 = x - 1

Û 4x - x = 13 - 1

Û 3x = 12

Û x = 4

Vậy tập nghiệm của phương trình là S = {4}.

Câu 6:

Giải các phương trình và bất phương trình sau:

b) |2x - 3| - 7 = 4;

Xem đáp án

b) |2x - 3| - 7 = 4

Û |2x - 3| = 4 + 7 = 11

$\Leftrightarrow [\begin{matrix} 2 x - 3 = 11 \\ 2 x - 3 = - 11 \end{matrix}$

$\Leftrightarrow [\begin{matrix} 2 x = 14 \\ 2 x = - 8 \end{matrix}$

$\Leftrightarrow [\begin{matrix} x = 7 \\ x = - 4 \end{matrix}$

Vậy tập nghiệm của phương trình là S = {-4; 7}.

Câu 7:

Giải các phương trình và bất phương trình sau:

c) $\frac{x - 5}{x + 1} + \frac{5}{x} = \frac{6}{x^{2} + x};$

Xem đáp án

c) $\frac{x - 5}{x + 1} + \frac{5}{x} = \frac{6}{x^{2} + x}$

$\Leftrightarrow \frac{x - 5}{x + 1} + \frac{5}{x} = \frac{6}{x (x + 1)}$

ĐKXĐ:

$\{\begin{matrix} x \neq 0 \\ x + 1 \neq 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x \neq 0 \\ x \neq - 1 \end{matrix}$

Khi đó phương trình đã cho tương đương với:

$\frac{x (x - 5)}{x (x + 1)} + \frac{5 (x + 1)}{x (x + 1)} = \frac{6}{x (x + 1)}$

$\Leftrightarrow \frac{x^{2} - 5 x}{x (x + 1)} + \frac{5 x + 5}{x (x + 1)} = \frac{6}{x (x + 1)}$

$\Leftrightarrow \frac{x^{2} + 5}{x (x + 1)} = \frac{6}{x (x + 1)}$

Þ x² + 5 = 6 Û x² = 1

Û x = ±1

Đối chiếu ĐKXĐ nên suy ra x = 1 là nghiệm của phương trình.

Vậy tập nghiệm của phương trình là S = {1}.

Câu 8:

Giải các phương trình và bất phương trình sau:

d) (x - 2)(x + 2) - x(x - 3) < x + 1.

Xem đáp án

d) (x - 2)(x + 2) - x(x - 3) < x + 1

Û x² - 4 - x² + 3x < x + 1

Û 3x - 4 < x + 1

Û 3x - x < 4 + 1

Û 2x < 5

Vậy tập nghiệm của bất phương trình là $S = \{x | x < \frac{5}{2}\} .$

Câu 9:

Giải bài toán sau bằng cách lập phương trình:

Một người đi xe máy từ A đến B với vận tốc trung bình 30 km/h. Khi tới B, người đó quay trở về A ngay với vận tốc trung bình 25 km/h. Biết tổng thời gian cả đi và về là 1giờ 6 phút. Tính quãng đường AB.

Xem đáp án

Hướng dẫn giải

Gọi x (km) là độ dài quãng đường AB (x > 0).

Thời gian ô tô đi từ A đến B với vận tốc 30 km/h là $\frac{x}{30} h$

Ô tô đi từ B về A với vận tốc 25 km/h với số thời gian là $\frac{x}{25} h$

Do tổng thời gian cả đi và về là 1giờ 6 phút, tức là $1 + \frac{6}{60} = \frac{11}{10} h$ nên ta có phương trình

$\frac{x}{30} + \frac{x}{25} = \frac{11}{10}$

$\Leftrightarrow \frac{5 x}{150} + \frac{6 x}{150} = \frac{11}{10}$

$\Leftrightarrow \frac{5 x + 6 x}{150} = \frac{11 x}{150} = \frac{11}{10}$

$\Leftrightarrow x = \frac{150}{11} . \frac{11}{10} = 15 (k m) .$

Vậy quãng đường AB dài 15 km.

Câu 10:

Một bể cá cảnh dạng hình hộp chữ nhật có chiều dài 25 cm, chiều rộng 15 cm, chiều cao 22 cm. Lúc đầu bể không có nước. Hỏi nếu người ta đổ vào bể 10 lít nước thì có đầy bể không? (bỏ qua bề dày thành bể).

Xem đáp án

Hướng dẫn giải

Thể tích của bể cá là:

25 . 15 . 22 = 8250 (cm³)

Đổi: 8250 cm³ = 8,25 lít.

Vì lúc đầu bể không có nước và 8,25 lít > 7 lít nên nếu đổ vào bể 7 lít nước thì bể không đầy.

Vậy nếu người ta đổ vào bể 10 lít nước thì không đầy bể.

Câu 11:

Cho tam giác ABC có ba góc nhọn, các đường cao BD và CE cắt nhau tại điểm H.

a) Chứng minh rằng: ∆ABD ᔕ ∆ACE;

Xem đáp án

Hướng dẫn giải

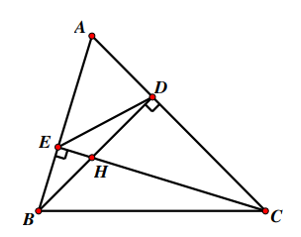
Cho tam giác ABC có ba góc nhọn, các đường cao BD và CE cắt nhau tại điểm H. a) Chứng minh rằng: ∆ABD ᔕ ∆ACE; (ảnh 1)

a) Xét ∆ABD và ∆ACE có:

$\begin{matrix} \hat{B A D} = \hat{C A E} (\hat{A} c h u n g) \\ \hat{A D B} = \hat{A E C} (= 90 °) \end{matrix}\} \Rightarrow Δ A B D ∽ Δ A C E (g . g)$

Câu 12:

b) Cho AB = 4 cm; AC = 5 cm; AD = 2 cm. Tính độ dài đoạn thẳng AE;

Xem đáp án

b) DABD ᔕ ∆ACE (cmt)

$\Rightarrow \frac{A B}{A C} = \frac{A D}{A E}$

$\Leftrightarrow A E = \frac{A C . A D}{A B} = \frac{5.2}{4} = 2,5 c m .$

Câu 13:

c) Chứng minh rằng: $\hat{E D H} = \hat{B C H} .$

Xem đáp án

c) DABD ᔕ ∆ACE (cmt)

$\Rightarrow \frac{A B}{A C} = \frac{A D}{A E} \Leftrightarrow \frac{A B}{A D} = \frac{A C}{A E}$

Xét ∆ADE và ∆ABC có :

$\begin{matrix} \hat{D A E} = \hat{B A C} (\hat{A} c h u n g) \\ \frac{A B}{A D} = \frac{A C}{A E} (c m t) \end{matrix}\} \Rightarrow Δ A D E ∽ Δ A B C (c . g . c)$

$\Rightarrow \hat{A D E} = \hat{A B C}$ (Hai góc tương ứng bằng nhau) (1)

Mà ta có:

+) $\hat{A D E} + \hat{E D H} = \hat{A D B} = 90 °$ (2)

+) $\hat{A B C} + \hat{B C H} = 180 ° - \hat{B E C} = 180 ° - 90 ° = 90 °$ (3)

Từ (1), (2) và (3) nên suy ra $\hat{E D H} = \hat{B C H} .$

Câu 14:

Cho hai số a, b thỏa mãn a + b ≠ 0. Chứng minh rằng:

$a^{2} + b^{2} + {(\frac{a b + 1}{a + b})}^{2} \geq 2.$

Xem đáp án

Hướng dẫn giải

Ta có: $a^{2} + b^{2} + {(\frac{a b + 1}{a + b})}^{2} \geq 2$

Û (a² + b²)(a + b)² + (ab + 1)² ³ 2(a + b)²

Û (a + b)²[(a + b)² - 2ab] + (ab + 1)² - 2(a + b)² ³ 0

Û (a + b)⁴ - 2ab(a + b)² + (ab + 1)² - 2(a + b)² ³ 0

Û (a + b)⁴ - 2(a + b)²(ab + 1) + (ab + 1)² ³ 0

Û [(a + b)² - (ab + 1)]² ³ 0 (luôn đúng "a, b)

Vậy suy ra $a^{2} + b^{2} + {(\frac{a b + 1}{a + b})}^{2} \geq 2 (\forall a, b) .$

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất)

Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương