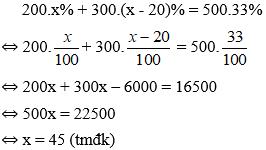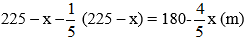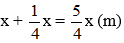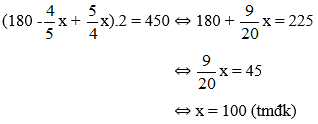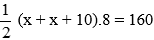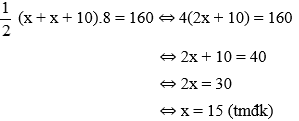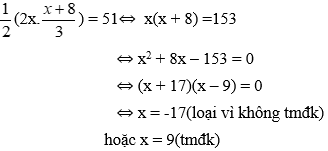13 câu hỏi trắc nghiệm thuộc Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán hình học, vật lí, hóa học

Câu 1:

Chu vi một khu vườn hình chữ nhật bằng 60m, hiệu độ dài của chiều dài và chiều rộng là 20m. Tìm độ dài các cạnh của hình chữ nhật.

Xem đáp án

Gọi chiều dài của khu vườn là x (m) (20 < x < 30)

Chiều rộng của khu vườn là x – 20 (m)

Chu vi của khu vườn bằng 60m nên ta có phương trình:

(x + x – 20). 2 = 60 ⇔ 2x – 20 = 30 ⇔ 2x = 50 ⇔ x = 25 (tmđk)

Vậy chiều dài của mảnh vườn là 25m, chiều rộng là 25 - 20 = 5m.

Câu 2:

Người ta pha 3kg nước nóng ở 90°C với 2kg nước lạnh ở 20°C. Tính nhiệt độ sau cùng của nước (bỏ qua sự mất nhiệt)

Xem đáp án

Gọi nhiệt độ sau cùng của nước là x°C (20 < x < 90)

Áp dụng công thức tính nhiệt lượng Q = m.c. Δt ta có:

Nhiệt lượng 3kg nước nóng tỏa ra đến khi cân bằng nhiệt là $Q_{t ỏ a} = 3.4200 (90 - x)$

Nhiệt lượng 2kg nước lạnh thu vào đến khi cân bằng nhiệt là $Q_{t h u} = 2.4200 (x - 20)$

Theo phương trình cân bằng nhiệt $Q_{t ỏ a} = Q_{t h u}$ nên ta có phương trình:

3.4200(90 – x) = 2.4200(x - 20)

⇔ 3(90 – x) = 2(x – 20)

⇔ 270 – 3x = 2x – 40 ⇔ 5x = 310

⇔ x = 62 (tmđk)

Vậy nhiệt độ sau cùng của nước là 62°C

Câu 3:

Có hai loại dung dịch muối I và II. Người ta hòa 200 gam dung dịch muối I với 300gam dung dịch muối II thì được một dung dịch có nồng độ muối là 33%. Tính nồng độ muối trong mỗi dung dịch I và II, biết rằng nồng độ muối trong dung dịch I lớn hơn nồng độ muối trong dung dịch II là 20%.

Xem đáp án

ọi nồng độ muối trong dung dịch I là x (%)(x > 20), nồng độ muối trong dung dịch II là x – 20(%)

Lượng muối có trong dung dịch I là 200.x%,

lượng muối có trong dung dịch II là 300.(x -20)%.

Theo định luật bảo toàn khối lượng ta có khối lượng dung dịch tạo thành là 200 + 300 = 500g

Theo bài ra ta có phương trình:

Vậy nồng độ mưới của dung dịch I là 45%, nồng độ muối của dung dịch II là 25%

Câu 4:

Một hình chữ nhật có chu vi 320m. Nếu tăng chiều dài 10m, tăng chiều rộng 20m thì diện tích tăng $2700 m^{2}$ . Tính chiều dài và chiều rộng của hình.

Xem đáp án

Gọi chiều rộng hình chũ nhật là x (m)(0 < x < 160)

Nửa chu vi hình chữ nhật là: 320:2 = 160 m

Chiều dài là 160 - x (m)

Diện tích của hình chữ nhật là: x (160 – x) $(m^{2})$

Khi tăng chiều dài thêm 10m và chiều rộng thêm 20m thì diện tích của hình là:

(x + 20)(160 – x + 10) = (x + 20)(170 – x)

Vì diện tích tăng $2700 m^{2}$ nên ta có phương trình:

x (160 – x) + 2700 = (x + 20)(170 – x)

$\Leftrightarrow 160 x - x^{2} + 2700 = 150 x - x^{2} + 3400$

⇔ 10x = 700 ⇔ x = 70 (tmđk)

Vậy hình chữ nhật có chiều rộng là 70m, chiều dài là 160 – x = 90m

Câu 5:

Một thửa đất hình chữ nhật có chu vi là 56m. Nếu giảm chiều rộng 2m và tăng chiều dài 4m thì diện tích tăng thêm $8 m^{2}$ . Tìm chiều rộng và chiều dài thửa đất.

Xem đáp án

Gọi chiều rộng của thửa đất là x (m) (x > 2)

Nửa chu vi của thửa đất là: 56:2 = 28(m)

Chiều dài của thửa đất là 28 – x (m)

Diện tích của thửa đất là x(28 – x) (m2)

Khi tăng chiều dài lên 4m, giảm chiều rộng đi 2m ta có diện tích là

(x – 2)(28 – x + 4) = (x – 2)(32 – x) ( $m^{2}$ )

Khi đó diện tích tăng thêm 8 $m^{2}$ nên ta có phương trình.

x(28 – x) + 8 = (x – 2)(32 – x))

$\Leftrightarrow 28 x - x^{2} + 8 = 34 x - x^{2} - 64$

⇔ 6x = 72 ⇔ x = 12 (tmđk)

Vậy chiều rộng của thửa đất là 12m, chiều dài thửa đất là 28 – 12 = 16m.

Câu 6:

Một khu vườn hình chữ nhật có chiều dài bằng 3 lần chiều rộng. Nếu tăng mỗi cạnh thêm 5m thì diện tích khu vườn tăng thêm $385 m^{2}$ . Tính độ dài các cạnh của khu vườn.

Xem đáp án

Gọi chiều rộng của mảnh vườn là x (m) (x > 0)

Chiều dài của mảnh vườn là 3x (m)

Diện tích mảnh vườn là $3 x . x = 3 x^{2}$

Khi tăng mỗi cạnh lên 5m thì diện tích mảnh vườn là: $(3 x + 5) (x + 5) = 3 x^{2} + 20 x + 25 .$

Khi đó diện tích tăng thêm $385 m^{2}$ nên ta có phương trình:

$3 x^{2} + 385 = 3 x^{2} + 20 x + 25$ ⇔ 20x = 360 ⇔ x = 18(tmđk)

Vậy chiều rộng của mảnh vườn là 18m, chiều dài của mảnh vườn là 18.3 = 54m

Câu 7:

Hiệu số đo chu vi của hai hình vuông là 32m và hiệu số đo diện tích của chúng là $464 m^{2}$ . Tìm số đo các cạnh của mỗi hình vuông.

Xem đáp án

Gọi độ dài cạnh của hình vuông nhỏ là x (m) (x > 0)

Chu vi hình vuông nhỏ là 4x (m)

Chu vi hình vuông lớn là 4x + 32

Độ dài cạnh hình vuông lớn là (4x + 32): 4 = 4(x + 8): 4 = x + 8 (m)

Diện tích hình vuông nhỏ là $x^{2} (m^{2})$

Diện tích hình vuông lớn là $(x + 8)^{2}$

Theo bài ra ta có phương trình:

$(x + 8)^{2} - x^{2} = 464 \Leftrightarrow x^{2} + 16 x + 64 - x^{2} = 464$

⇔ 16x = 400 ⇔ x = 25 (tmđk)

Vậy cạnh hình vuông nhỏ là 25m; cạnh hình vuông lớn là 25 + 8 = 33m.

Câu 8:

Một khu vườn hình chữ nhật có chu vi là 450m. Nếu giảm chiều dài đi $\frac{1}{5}$ chiều dài cũ và tăng chiều rộng thêm $\frac{1}{4}$ chiều rộng cũ thì chu vi hình chữ nhật không đổi. Tính chiều dài và chiều rộng khu vườn.

Xem đáp án

Gọi chiều rộng của khu vườn là x (m) (x > 0)

Nửa chu vi của hình chữ nhật là: 450 : 2 = 225 m

Chiều dài của khu vườn là 225 – x (m)

Khi giảm chiều dài đi 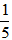chiều dài cũ ta được chiều dài mới là:

Khi tăng chiều rộng thêm 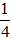chiều rộng cũ thì ta được chiều rộng mới là

Khi đó chu vi hình chữ nhật không đổi nghĩa là ta có phương trình:

Vậy chiều rộng của khu vườn là 100m, chiều dài của khu vườn là 125m.

Câu 9:

Một khu đất hình chữ nhật có chiều dài hơn chiều rộng là 10m. Nếu chiều dài tăng thêm 6m, chiều rộng giảm đi 3m thì diện tích mới tăng hơn diện tích cũ là $12 m^{2}$ . Tính các kích thước của khu đất.

Xem đáp án

Gọi chiều rộng của khu đất là x (m) (x > 3)

Chiều dài của khu đất là x + 10 (m)

Diện tích của khu đất là x(x + 10) ( $m^{2}$ )

Khi tăng chiều dài thêm 6m thì chiều dài của khu đất là x + 10 + 6 = x + 16 (m)

Khi giảm chiều rộng đi 3m thì chiều rộng của khu đất là x - 3 (m)

Diện tích của khu đất lúc này là (x – 3)(x + 16)

Vì diện tích mới tăng hơn diện tích cũ là 12 $m^{2}$ nên ta có phương trình:

(x – 3)(x + 16) = x(x + 10) + 12

$\Leftrightarrow x^{2} + 13 x - 48 = x^{2} + 10 x + 12$

⇔ 3x = 60

⇔ x = 20 (tm đk)

Vậy chiều rộng của khu đất là 20 m, chiều dài của khu đất là 20 + 10 = 30m

Câu 10:

Hai cạnh của một hình bình hành có độ dài là 6cm và 8cm. Đường cao ứng với cạnh 6cm có độ dài là 5cm. Tính độ dài đường cao thứ hai?

Xem đáp án

Gọi x (cm) là độ dài đường cao thứ hai ứng với cạnh 8cm của hình bình hành (0 < x < 5)

Theo công thức tính diện tích hình bình hành ta có phương trình:

6.5 = 8.x ⇔ 8x =30 ⇔ x = 3,75 (tmđk)

Vậy độ dài đường cao thứ hai là 3,75cm

Câu 11:

Một hình thang có diện tích $160 c m^{2}$ , đường cao bằng 8cm. Tính độ dài mỗi đáy hình thang biết hai đáy hơn kém nhau 10cm.

Xem đáp án

Gọi chiều dài đáy nhỏ của hình thang là x (cm) (x > 0)

Chiều dài đáy lớn là x + 10 (cm)

Diện tích hình thang là $160 c m^{2}$

Theo công thức tính diện tích hình thang ta có phương trình:

Giải phương trình:

Vậy chiều dài đáy nhỏ của hình thang là 15cm, chiều dài đáy lớn của hình thang là 25cm.

Câu 12:

Một mảnh đất hình chữ nhật có chiều dài hơn chiều rộng 6m, và bình phương độ dài đường chéo gấp 5 lần chu vi. Xác định chiều dài và chiều rộng mảnh đất?

Xem đáp án

Gọi chiều dài mảnh đất là x (m)(x > 6)

Chiều rộng mảnh đất là x – 6 (m)

Chu vi mảnh đất là 2(x + x – 6) = 4x – 12 (m)

Theo định lí Py-ta-go ta có bình phương đường chéo của mảnh đất là $x^{2} + (x - 6)^{2}$

Vì bình phương đường chéo gấp 5 lần chu vi nên ta có phương trình:

$x^{2} + (x - 6)^{2} = 5 (4 x - 12) \Leftrightarrow x^{2} + x^{2} - 12 x + 36 = 20 x - 60$

$\Leftrightarrow 2 x^{2} - 32 x + 96 = 0 \Leftrightarrow x^{2} - 16 x + 48 = 0$

⇔ (x – 12)(x – 4) = 0 ⇔ x = 12 (tmđk) hoặc x = 4 (không tmđk x > 6)

Vậy chiều dài của mảnh đất là 12m, chiều rộng của mảnh đất là 6m

Câu 13:

Một tam giác vuông có hai cạnh góc vuông hơn kém nhau 8m, nếu tăng độ dài cạnh góc vuông nhỏ lên 2 lần và giảm độ dài cạnh góc vuông còn lại xuống 3 lần thì được tam giác vuông mới có diện tích bằng $51 m^{2}$ .Tính độ dài hai cạnh góc vuông?

Xem đáp án

Gọi độ dài cạnh góc vuông nhỏ là x (m)(x > 0)

Độ dài cạnh góc vuông lớn là x + 8 (m)

Khi tăng độ dài cạnh góc vuông nhỏ lên 2 lần ta được cạnh có độ dài 2x (m)

Khi giảm độ dài cạnh góc vuông còn lại xuống 3 lần thì được cạnh có độ dài 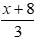(m)

Tam giác vuông mới có diện tích bằng $51 m^{2}$

Theo công thức tính diện tích tam giác vuông ta có phương trình:

Vậy độ dài cạnh góc vuông nhỏ là 9m. Độ dài cạnh góc vuông lớn là 17m.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Tổng hợp bài tập Toán 8 Chương 3: Phương trình bậc nhất một ẩn

Cách giải bài toán bằng cách lập phương trình cực hay: Bài toán hình học, vật lí, hóa học

Danh sách câu hỏi

Bài thi liên quan

Các bài thi hot trong chương