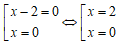Cách chứng minh hai phương trình tương đương cực hay, có đáp án
-
5143 lượt thi
-
18 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Xét xem các phương trình sau có tương đương không? 3x = 3 và x – 1 = 0
Ta có 3x = 3 ⇔ 3x – 3 = 0 ⇔ 3(x – 1) = 0 ⇔ 3(x – 1) : 3 = 0 : 3 ⇔ x – 1 = 0
Vậy 3x = 3 ⇔ x – 1 = 0
Câu 2:
Xét xem các phương trình sau có tương đương không? x + 3 = 0 và 3x + 9 = 0
Ta có x + 3 = 0 ⇔ 3(x + 3) = 0.3 ⇔ 3x + 9 = 0
Vậy x + 3 = 0 ⇔ 3x + 9 = 0.
Câu 3:
Xét xem các phương trình sau có tương đương không? x - 2 = 0 và (x - 2)(x - 3) = 0
Phương trình x – 2 = 0 có tập nghiệm S = {2},
phương trình (x - 2)(x - 3) = 0 có tập nghiệm S = {2; 3}
Vậy 2 phương trình x - 2 = 0 và (x - 2)(x - 3) = 0 không tương đương
Câu 4:
Xét xem các phương trình sau có tương đương không? 2x - 6 = 0 và x(x - 3) = 0
Phương trình 2x – 6 = 0 ⇔ 2x = 6 ⇔ x = 3
⇒ phương trình 2x – 6 = 0 có tập nghiệm S = {3}
Phương trình x(x – 3) = 0 có tập nghiệm S = {0;3}
Vậy 2 phương trình 2x - 6 = 0 và x(x - 3) = 0 không tương đương
Câu 5:
Xét xem hai phương trình x + 2 = 0 và có tương đương không?
Ta có x = -2 là nghiệm của phương trình x + 2 = 0.
Với x = -2 phương trình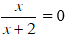 
vô nghĩa.
Vậy hai phương trình đã cho không tương đương.
Câu 6:
Phương trình x – 1 = 0 tương đương với phương trình nào trong các phương trình sau?
Chọn A
Ta có x – 1 = 0 ⇔ x = 1.
Câu 7:
Phương trình 3x – 6 = 0 tương đương với phương trình nào sau đây
Chọn D
Ta có (1) giải PT: 3x – 6 = 0 ⇔ 3x = 6 ⇔ x = 2.
phương trình 3x – 6 = 0 có tập nghiệm S = {2}
(2) giải PT: ⇔ (x + 2)(x – 2) = 0 ⇔ 
Phương trình có tập nghiệm S = {-2;2}
(3) giải PT: x – 6 = 0 ⇔ x = 6
Phương trình x - 6 = 0 có tập nghiệm S = {6}
(4) Phương trình x = 3 có tập nghiệm S = {3}
(5) giải PT: ⇔ x – 2 = 0 (vì với mọi x)
⇔ x = 2
Phương trình có tập nghiệm S = {2}
Vậy PT 3x – 6 = 0 tương đương với phương trình vì có cùng tập nghiệm.
Câu 8:
Trong các khẳng định sau, khẳng định nào đúng.
Chọn B
Ta có 3x + 2 = x + 8 ⇔ 2(3x + 2) = 2(x + 8) ⇔ 6x + 4 = 2x + 16.
Vậy 3x + 2 = x + 8 và 6x + 4 = 2x + 16 là hai phương trình tương đương.
Câu 9:
Trong các khẳng định sau, khẳng định nào sai?
Chọn C
Ta có 2x – 4 = 0 ⇔ 2x = 4 ⇔ x = 2; ⇔ x = 2 hoặc x = -2;
Vậy hai phương trình 2x – 4 = 0 và không có cùng tập nghiệm, là hai phương trình không tương đương.
Câu 10:
Xét sự tương đương của các phương trình sau ? 18x + 5 = 8x + 15 và 10x = 10
Ta có 18x + 5 = 8x +15 ⇔ 18x – 8x = 15 – 5 ⇔ 10x = 10.
Vậy 2 phương trình 18x + 5 = 8x + 15 và 10x = 10 là tương đương.
Câu 11:
Xét sự tương đương của các phương trình sau ? 2x – 1 = 2 và (2x – 1)x = 2x
Ta có: (1) 2x – 1 = 2 ⇔ 2x = 3 ⇔ x = 
Phương trình 2x – 1 = 2 có tập nghiệm S = {};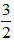
(2) (2x – 1)x = 2x ⇔ (2x – 1)x - 2x = 0 ⇔ x(2x - 1 – 2) = 0
⇔ x (2x - 3) = 0 ⇔ x = 0 hoặc 2x = 3 ⇔ x = 0 hoặc x =
Phương trình (2x – 1)x = 2x có tập nghiệm S = { 0; }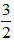
Vậy hai phương trình 2x – 1 = 2 và (2x – 1)x = 2x không tương đương vì không có cùng tập nghiệm
Câu 12:
Xét sự tương đương của các phương trình sau ? 2x - 3 = 9 và (2x - 3)x = 9x
Ta có 2x - 3 = 9 ⇔ 2x = 12 ⇔ x = 6;
(2x - 3)x = 9x ⇔ 2x(x – 6) = 0 ⇔ x = 0 hoặc x = 6.
Vậy hai phương trình 2x - 3 = 9 và (2x - 3)x = 9x không tương đương vì không có cùng tập nghiệm
Câu 13:
Xét sự tương đương của các phương trình sau ? │3x│ = 6 và │x│ = 2.
Ta có │3x│ = 6 ⇔ 3│x│ = 6 ⇔ │ x│ = 2.
Vậy 2 phương trình │3x│ = 6 và │x│ = 2 là tương đương.
Câu 14:
Chứng minh hai phương trình và x + 3 = 4x + 4 tương đương
Ta có: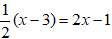 
⇔ x – 3 = 4x – 2 ⇔ x – 3 + 6 = 4x – 2 + 6 ⇔ x + 3 = 4x + 4.
Vậy hai phương trình 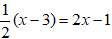và x + 3 = 4x + 4 tương đương.
Câu 15:
Khẳng định và 2x = 4 là hai phương trình tương đương đúng hay sai ? Vì sao ?
Khẳng định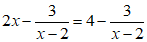 
và 2x = 4 là hai phương trình tương đương là sai.
Vì phương trình 2x = 4 có nghiệm x = 2. Nhưng với x = 2 thì phân thức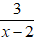 
vô nghĩa.
Vậy x = 2 không là nghiệm của phương trình .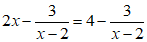
Câu 16:
Xét xem các phương trình sau có tương đương hay không? x + 1 = x và
Ta có x + 1 = x ⇔ 0x = 1 (vô lí) ⇒ phương trình vô nghiệm;
(vô lí) ⇒ phương trình vô nghiệm
⇒ Hai phương trình x + 1 = x và tương đương vì có cùng tập nghiệm.
Câu 17:
Xét xem các phương trình sau có tương đương hay không? x + 2 = 2 và (x + 2)(x – 2)= 2(x - 2)
Ta có:
x + 2 = 2 ⇔ x = 2 – 2 ⇔ x = 0
PT x + 2 = 2 có tập nghiệm S = { 0}
(x + 2)(x – 2)= 2(x - 2)
⇔ (x + 2)(x – 2) - 2(x - 2) = 0
⇔ (x – 2)(x + 2 – 2) = 0
⇔ (x – 2)x = 0
⇔ 
Pt (x + 2)(x – 2)= 2(x - 2) có tập nghiệm S = {0;2}
Vậy hai phương trình x + 2 = 2 và (x + 2)(x – 2)= 2(x - 2) không tương đương vì không có cùng tập nghiệm.
Câu 18:
Chứng minh các phương trình │x - 1│ = 2 và (x + 1)(x - 3) = 0 tương đương
Ta có │x - 1│ = 2 ⇔ x – 1 = -2 hoặc x – 1 = 2 ⇔ x = -1 hoặc x = 3;
(x + 1)(x - 3) = 0 ⇔ x + 1 = 0 hoặc x – 3 = 0 ⇔ x = -1 hoặc x = 3.
Vậy hai phương trình │x - 1│ = 2 và (x + 1)(x - 3) = 0 tương đương vì có cùng tập nghiệm