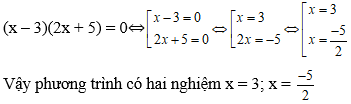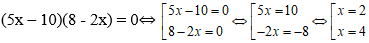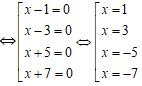Cách giải phương trình tích cực hay, có đáp án
-
5520 lượt thi
-
23 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Giải các phương trình sau: (x + 1)(3x – 3) = 0
Vậy phương trình đã cho có tập nghiệm là S ={-1; 1}
Câu 2:
Giải các phương trình sau: (2x + 4)(x + 3) = 0.
Vậy phương trình đã cho có tập nghiệm là S ={-2; -3}
Câu 7:
Giải các phương trình sau: (x – 2)(3x + 5) = (2x - 4)(x +1)
Vậy phương trình đã cho có tập nghiệm là S ={-3; 2}
Câu 10:
Tập nghiệm của phương trình (5x – 10)(8 - 2x) = 0 là
Chọn D
Vậy phương trình có tập nghiệm S = { 2; 4}.
Câu 12:
Phương trình (9 – 3x)(15 + 3x) = 0 có tập nghiệm là:
Chọn C
(9 – 3x)(15 + 3x) = 0 ⇔ 9 - 3x = 0 hoặc 15+ 3x = 0 ⇔ -3x = -9 hoặc 3x = -15
⇔ x = 3 hoặc x = -5
Vậy phương trình có hai nghiệm x = - 5 và x = 3.
Câu 13:
Tập nghiệm của phương trình (2x + 5)(x – 4) = (x – 5)(4 – x) là
Chọn B
Ta có: (2x + 5)(x – 4) = (x – 5)(4 – x)
⇔ (2x + 5)(x – 4) - (x – 5)(4 – x) = 0
⇔ (2x + 5)(x – 4) + (x – 5)(x – 4) = 0
⇔ (x – 4)(2x + 5 + x – 5) = 0⇔ (x – 4)3x = 0
⇔ 3x = 0 hoặc x – 4 = 0 ⇔ x = 0 hoặc x = 4
Vậy phương trình có hai nghiệm x = 0 và x = 4.
Câu 14:
Giải các phương trình sau: (x – 3)(2x + 1) = 0
(x – 3)(2x + 1) = 0 ⇔ x – 3 = 0 hoặc 2x + 1 = 0
⇔ x = 3 hoặc 2x = -1 ⇔ x = 3 hoặc x = -1/2
Vậy phương trình có hai nghiệm x = -1/2 và x = 3.
Câu 15:
Giải các phương trình sau: (3x + 4)(5 – x) = 0
(3x + 4)(5 – x) = 0 ⇔ 3x +4 = 0 hoặc 5 - x = 0 ⇔ 3x = -4 hoặc –x = -5
⇔ x = -4/3 hoặc x = 5
Vậy phương trình có hai nghiệm x = -4/3 và x = 5.
Câu 20:
Giải các phương trình sau:
⇔ (3x – 2)(3x + 2)(x + 1) - (3x + 2)(x - 1)(x + 1) = 0
⇔(3x+ 2)(x + 1)(3x – 2 – x + 1) = 0
⇔ (3x + 2)(x + 1)(2x – 1) = 0
Câu 23:
Giải các phương trình sau: (x – 1)(x – 3)(x + 5)(x + 7) = 0
(x – 1)(x – 3)(x + 5)(x + 7) = 0
Vậy tập nghiệm của phương trình là S = { -7;-5;1;3}