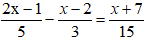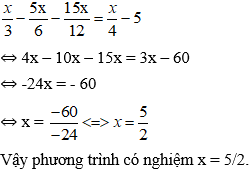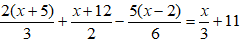Cách giải phương trình đưa được về dạng ax + b = 0 cực hay, có đáp án
-
5491 lượt thi
-
21 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Giải các phương trình sau 5 – (6 – x) = 4(3 – 2x)
5 – (6 – x) = 4(3 – 2x)
⇔ 5 – 6 + x = 12 – 8x
⇔ x + 8x = 12 – 5 + 6
⇔ 9x = 13
⇔ x = 13/9
Vậy phương trình có một nghiệm x = 13/9.
Câu 2:
Giải các phương trình sau 4(x – 4) = -7x +17
4(x – 4) = -7x +17
⇔ 4x - 16 = -7x + 17
⇔ 4x + 7x = 17 + 16
⇔ 11x = 33
⇔ x = 3
Phương trình có tập nghiệm S = { 3}
Câu 3:
Giải các phương trình sau 2(x – 3) = -3(x – 1) + 7.
2(x – 3) = -3(x – 1) + 7.
⇔ 2x – 6 = -3x + 3 + 7
⇔ 5x = 16
⇔
Vậy phương trình có tập nghiệm S = {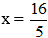
Câu 4:
Giải các phương trình sau 4(3x – 2) – 3(x - 4) = 7x + 20.
4(3x – 2) – 3(x - 4) = 7x + 20.
⇔ 12x – 8 – 3x + 12 = 7x + 20
⇔ 9x – 7x = 20 + 8 – 12
⇔ 2x = 16
⇔ x = 8
Vậy phương trình có tập nghiệm S = { 8}
Câu 5:
Giải các phương trình sau:
⇔ 3(2x – 1) – 5(x - 2) = x + 7
⇔ 6x – 3 – 5x + 10 = x + 7
⇔ x – x = 7- 7
⇔ 0x = 0 (pt thỏa mãn với mọi x)
Vậy phương trình đã cho có vô số nghiệm.
Câu 7:
Phương trình 5 - (2 – x) = 4(3 – 2x) có tập nghiệm là:
Đáp án: A.
5 - (2 – x) = 4(3 – 2x) ⇔ 5 – 2 + x = 12 - 8x ⇔ x + 8x = 12 – 3⇔ 9x = 9 ⇔ x = 1
Vậy phương trình có nghiệm x = 1.
Câu 8:
Phương trình 5(x – 3) - 4 = 2(x – 1) +7 có tập nghiệm là:
Đáp án: C.
5(x – 3) - 4 = 2(x – 1) +7 ⇔ 5x – 15 – 4 = 2x – 2+ 7
⇔ 5x – 2x = 5 + 19 ⇔ 3x = 24 ⇔ x = 8
Vậy phương trình có nghiệm x = 8.
Câu 10:
Giá trị x = 4 là nghiệm của phương trình nào trong các phương trình sau:
Đáp án: B
Cách 1: Thay x = 4 vào các phương trình ta được:
A. 7 – 3.4 ≠ 9 - 4 ⇔ -5 ≠ 5
B. 2(3.4 + 1) + 4 = 5(4 + 2) ⇔ 30 = 30
C. 2.4 – (3 – 5.4) ≠ 2(4 +3) ⇔ 25 ≠ 14
D. ⇔ 96 ≠ 23
Cách 2:
Giải các phương trình ta được
A. 7 – 3x = 9 - x ⇔ -3x + x = 9 - 7 ⇔ -2x = 2 ⇔ x = -1
B. 2(3x + 1) + 4 = 5(x + 2) ⇔ 6x + 2 + 4 = 5x + 10 ⇔ x = 10 -2 – 4⇔ x = 4
C. 2x – (3 – 5x) = 2(x +3) ⇔ 2x – 3+ 5x = 2x + 6⇔ 5x = 6 + 3 ⇔ x = 9/5
D. ⇔ 24x = 5x + 3 ⇔ 19x = 3 ⇔ x = 3/19.
Vậy x = 4 là nghiệm của phương trình 2(3x + 1) + 4 = 5(x + 2).
Câu 11:
Phương trình có tập nghiệm:
Chọn D
⇔ 4(x + 5) + 3(x + 12) - 5(x – 2) = 2x + 66
⇔ 4x + 20 + 3x + 36 – 5x + 10 = 2x + 66
⇔ 0x = 0 (thỏa mãn mọi giá trị của x)
Vậy phương trình đã cho có vô số nghiệm.
Câu 12:
Giải các phương trình sau: 3x – 2 = 5(x + 1)
3x – 2 = 5(x + 1) ⇔ 3x – 2 = 5x + 5 ⇔ 3x – 5x = 5 +2 ⇔ -2x = 7 ⇔ x = -3,5
Vậy phương trình có nghiệm x = -3,5.
Câu 13:
Giải các phương trình sau: 2x –(5x + 3) = 4(3x – 1) -7.
2x –(5x + 3) = 4(3x – 1) -7 ⇔ 2x – 5x – 3 = 12x- 4 – 7 ⇔ - 15x = -8 ⇔ x = 8/15
Vậy phương trình có nghiệm x = 8/15.